Back to .NET Basics: How to properly use HttpClient

https://www.tpeczek.com/2019/10/alternative-approach-to-httpclient-in.html

Alternative approach to HttpClient in AZURE Functions 2.0 revisited – move to dependency injection

https://github.com/tpeczek

Hi there 👋, I"m Tomasz Pęczek

Software Developer & Architect • Blogger • Speaker • OSS Contributor • Microsoft MVP

https://www.youtube.com/watch?v=OcCKmodXW-Q

Likes: 254

http://danpatrascu.com/, https://github.com/danpdc/aspNetCoreBeginners,

Asp.Net Core Authorization Made Easy

http://danpatrascu.com/

https://github.com/danpdc/aspNetCoreBeginners

https://blog.joaograssi.com/posts/2021/asp-net-core-deep-dive-policy-based-authorization/

Stars: 82

https://github.com/joaopgrassi/authz-custom-middleware/tree/posts/policy-based-deep-dive ,

This second lesson of the “ASP.Net Core for beginners” course is almost entirely hands on. We will satrt implementing our API, by first setting up our project structure according to a layered architecture. We will implement our first endpoints and we will then talk about dependency injection.

https://www.codeproject.com/Articles/1162957/Dependency-Injection-to-The-Core

We can go further and build a composition root where we can do this kind of type initializations. The composition root is a simple class which will get called when the application is first initialized. In that class, we can resolve the specific types for our abstractions.

As you can see here, we have configured our HTTPRequest in such a way that if someone requests the TodoControllerwe will instantiate a new instance of TodoRepository and pass it to the controller's constructor. Likewise, we can change it toTodoCSVRepository or TodoInMemoryepository whenever we feel like. Now we have a single place to do all our dirty works of type initializations. In Web API projects we have to register this composition root in the Global.asax.cs file like this,

Can_someone_explain_when_to_use_singleton_scoped

r/csharp Can someone explain when to use Singleton, Scoped and Transient?

https://www.reddit.com/r/csharp/comments/1acwtar/can_someone_explain_when_to_use_singleton_scoped/

Preparingtocode•

7mo ago

Singleton: This creates only one instance of a class during the application's lifecycle. Every time you request this class, you get the same instance. Use it for classes that are expensive to create or maintain a common state throughout the application, like a database connection.

Transient: Every time you request a transient class, a new instance is created. This is useful for lightweight, stateless services where each operation requires a clean and independent instance.

Scoped: Scoped instances are created once per client request. In a web application, for example, a new instance is created for each HTTP request but is shared across that request. Use it for services that need to maintain state within a request but not beyond it, like shopping cart in an e-commerce site.

▲114▼ReplyAwardShare⋯

mcb2001•

7mo ago

Ef core is a unit of work pattern in it self, and should always be scoped

▲41▼ReplyAwardShare

jordansrowles•

8mo ago

This is the default object lifetime for the AddDbContext() method

▲13▼ReplyAwardShare

Dennis_enzo•

8mo ago

Always? No. It wholly depends on the scope. In blazor server side, the scope is the entire duration of the client connection. You really don't want to use the same dbcontext over and over again in that period.

▲8▼ReplyAwardShare

theiam79•

7mo ago

That 's when you should start using DbContextFactory instead

▲2▼ReplyAwardShare

Tags:

C# Azure TelemetryClient will leak memory if not implemented as a singleton

Accordion

C# Azure TelemetryClient will leak memory if not implemented as a singleton

C# Azure TelemetryClient will leak memory if not implemented as a singleton07/05/20

I noticed that my classic .net web application would leak memory after I implemented metrics for some background tasks.

Further investigation showed that my MetricAggregationManager would not release its memory.

Since one of the major changes was the implementation of a TelemetryClient, and since the memory not being released was from the Microsoft.ApplicationInsights.Metrics namespace, I concluded that the problem lies within the creation of the TelemetryClient:

using System;
using Microsoft.ApplicationInsights;
using Microsoft.ApplicationInsights.Metrics;
 
namespace MyCode
{
  public class BaseProcessor
  {
    private readonly TelemetryClient _telemetryClient;
     
    private BaseProcessor()
    {
      string instrumentationKey = "somekey"
      var telemetryConfiguration = new TelemetryConfiguration { InstrumentationKey = instrumentationKey };
      // This is a no-go. I should not create a new instance for every BaseProcessor
      _telemetryClient = new TelemetryClient(telemetryConfiguration);
    }
  }
}

The code above will create a new TelemetryClient for each creation of my base class. The TelemetryClient will collect metrics and store those in memory until either a set time or number of metrics are met, and then dump the metrics to Application Insights.

Tags: C# Azure TelemetryClient will leak memory if not implemented as a singleton

Hey, I'm Steven, a .NET Developer, andFreelancer in Zurich, Switzerland. I am a Microsoft MVP.

Also, this blog is open source onGitHub.

• xUnit v3 and some stuff about TUnit
• Fullstack Web Applications with .NET, Nx and Angular Seminar(Sep 27, 2024)
• Swagger Replacement in ASP.NET 9(Sep 23, 2024)
• Managing TaskCancellationTokens in a central service in ASP.NET(Sep 16, 2024)
• LINQ Joins on multiple columns in Entity Framework(Sep 09, 2024)
• How to test HttpClient inside API Tests(Sep 02, 2024)
• To Soft Delete or Not to Soft Delete(Aug 26, 2024)
• FormattableStringFactory - Creating dynamic FormattableString instances(Aug 19, 2024)
• async2 - The .NET Runtime Async experiment concludes(Aug 12, 2024)
• Organizing Parameters in Minimal API with the AsParametersAttribute(Aug 05, 2024)
• How many APIs does .NET have?(Jul 29, 2024)
• The state machine in C# with async/await(Jul 22, 2024)
• How not to benchmark!(Jul 15, 2024)
• UUID v7 in .NET 9(Jul 08, 2024)
• Codespaces for your open-source project(Jul 02, 2024)
• ReadOnlySet<T> in .NET 9(Jun 26, 2024)
• NCronJob - June Edition(Jun 21, 2024)
• Are my EF LINQ to SQL queries safe?(Jun 17, 2024)
• Does an HttpClient await the Header and the body?(Jun 10, 2024)
• Solving Duplicate Requests in Microservices(May 27, 2024)
• Pipeline in ASP.NET 6(May 20, 2024)

Awesome .NET!

A collection of awesome .NET libraries, tools, frameworks and software

https://stackoverflow.com/users/2281790/harald-coppoolse

About

Taught by Professor Dijkstra, so I'm conditioned like a Maslov dog to make software how it "ought" to be done, not for fast hacks, which sometimes is a drawback, except if you're working in projects with a lot of people that need to keep working for years and years continuously changing it.

https://github.com/MikaelGRA/InfluxDB.Client

About

InfluxDB Client for .NET. Timeseries Database - InfluxDB which is very popular and used in many .NET applications.

InfluxDB Client for .NET

    public class ComputerInfo
    {
       [InfluxTimestamp]
       public DateTime Timestamp { get; set; }
    
       [InfluxTag( "host" )]
       public string Host { get; set; }
    
       [InfluxTag( "region" )]
       public string Region { get; set; }
    
       [InfluxField( "cpu" )]
       public double CPU { get; set; }
    
       [InfluxField( "ram" )]
       public long RAM { get; set; }
    }
    

private ComputerInfo[] CreateTypedRowsStartingAt( DateTime start, int rows )
{
    var rng =  new Random();
    var regions = new[] { "west-eu", "north-eu", "west-us", "east-us", "asia" };
    var hosts = new[] { "some-host", "some-other-host" };

    var timestamp = start;
    var infos = new ComputerInfo[ rows ];
    for ( int i = 0 ; i < rows ; i++ )
    {
        long ram = rng.Next( int.MaxValue );
        double cpu = rng.NextDouble();
        string region = regions[ rng.Next( regions.Length ) ];
        string host = hosts[ rng.Next( hosts.Length ) ];

        var info = new ComputerInfo { Timestamp = timestamp, CPU = cpu, RAM = ram, Host = host, Region = region };
        infos[ i ] = info;

        timestamp = timestamp.AddSeconds( 1 );
    }

    return infos;
}

public async Task Should_Write_Typed_Rows_To_Database()
{
    var client = new InfluxClient( new Uri( "http://localhost:8086" ) );
    var infos = CreateTypedRowsStartingAt( new DateTime( 2010, 1, 1, 1, 1, 1, DateTimeKind.Utc ), 500 );
    await client.WriteAsync( "mydb", "myMeasurementName", infos );
}

Author of Blog: Mikael Guldborg Rask Andersen

Stars: 103

https://stackoverflow.com/questions/53811620/pull-data-from-multiple-tables-in-one-sql-query-using-linq-and-entity-framework

Pull data from multiple tables in one SQL query using LINQ and Entity Framework(Core)

Answerd by: https://stackoverflow.com/users/2281790/harald-coppoolse

I wanted to grab the 10 latest transactions and 10 latest customers in one LINQ query

It is a bit unclear what you want. I doubt that you want one sequence with a mix of Customers and Transactions. I guess that you want the 10 newest Customers, each with their last 10 Transactions?

I wonder why you would deviate from the entity framework code first conventions. If your class Customer represents a row in your database, then surely it doesn't have a HashSet <Transaction>?

A one-to-many of a Customer with his Transactions should be modeled as follows:

class Customer
{
    public int Id {get; set;}
    ... // other properties

    // every Customer has zero or more Transactions (one-to-many)
    public virtual ICollection<Transaction> Transactions {get; set;}
}
class Transaction
{
    public int Id {get; set;}
    ... // other properties

    // every Transaction belongs to exactly one Customer, using foreign key
    public int CustomerId {get; set;}
    public virtual Customer Customer {get; set;}
}

public MyDbContext : DbContext
{
    public DbSet<Customer> Customers {get; set;}
    public DbSet<Transaction> Transactions {get; set;}
}
            

This is all that entity framework needs to know to detect the tables you want to create, to detect your one-to-many relationship, and to detect the primary keys and foreign keys. Only if you want different names of tables or columns, you'll need attributes and/or fluent API The major differences between my classes and yours, is that the one-to-many relation is represented by virtual properties. The HashSet is an ICollection. After all, your Transactions table is a collection of rows, not a HashSet

In entity framework the columns of your tables are represented by non-virtual properties; the virtual properties represent the relations between the tables (one-to-many, many-to-many, ...)

Quite a lot of people tend to (group-)join tables, when they are using entity framework. However, life is much easier if you use the virtual properties

Back to your question

I want (some properties of) the 10 newest Customers, each with (several properties of) their 10 latest Transactions

var query = dbContext.Customers                           // from the collection of Customer
.OrderByDescending(customer => customer.Created)      // order this by descending Creation date
.Select(customer => new                               // from every Customer select the
{                                                     // following properties
     // select only the properties you actually plan to use
     Id = Customer.Id,
     Created = Customer.Created,
     Name = Customer.Name,
     ...

     LatestTransactions = customer.Transactions        // Order the customer's collection
         .OrderBy(transaction => transaction.Created)  // of Transactions
         .Select(transaction => new                    // and select the properties
         {
             // again: select only the properties you plan to use
             Id = transaction.Id,
             Created = transaction.Created,
             ...

             // not needed you know it equals Customer.Id
             // CustomerId = transaction.CustomerId,
         })
         .Take(10)                                      // take only the first 10 Transactions
         .ToList(),
})
.Take(10);                                              // take only the first 10 Customers

Entity framework knows the one-to-many relationship and recognizes that a group-join is needed for this.

One of the slower parts of your query is the transfer of the selected data from the DBMS to your local process. Hence it is wise to limit the selected data to the data you actually plan to use. If Customer with Id 4 has 1000 Transactions, it would be a waste to transfer the foreign key for every Transaction, because you know it has value 4.

https://www.entityframeworktutorial.net/code-first/code-first-conventions.aspx

These EF 6.x Code-First conventions are defined in the System.Data.Entity.ModelConfiguration.Conventions namespace.

The following table lists default code first conventions:

Extra_End

https://github.com/dotnet/EntityFramework.Docs/blob/main/entity-framework/core/modeling/relationships/one-to-many.md

https://github.com/dotnet/EntityFramework.Docs

Stars: 1.5k

title: One-to-many relationships - EF Core description: How to configure one-to-many relationships between entity types when using Entity Framework Core author: ajcvickers ms.date: 03/30/2023 uid: core/modeling/relationships/one-to-many

Extra_End

https://codeblog.jonskeet.uk/2019/03/27/storing-utc-is-not-a-silver-bullet/27/3/2019

STORING UTC IS NOT A SILVER BULLET

Note: this is a pretty long post. If you are not interested in the details, the conclusion at the bottom is intended to be read in a standalone fashion. There is also a related blog post by Lau Taarnskov https://www.creativedeletion.com/2015/03/19/persisting_future_datetimes.html - if you find this one difficult to read for whatever reason, maybe give that a try.

When I read Stack Overflow questions involving time zones, there 's almost always someone giving the advice to only ever store UTC. Convert to UTC as soon as you can, and convert back to a target time zone as late as you can, for display purposes, and you 'll never have a time zone issue again, they say.

This blog post is intended to provide a counterpoint to that advice. I'm certainly not saying storing UTC is always the wrong thing to do, but it s not always the right thing to do either. Note on simplifications: this blog post does not go into supporting non-Gregorian calendar systems, or leap seconds. Hopefully developers writing applications which need to support either of those are already aware of their requirements.

Background: EU time zone rule changes

The timing of this blog post is due to recent European Parliament proceedings that look like they will probably end the clocks changing twice a year into “summer time” or “winter time” within EU member states. The precise details are yet to be finalized and are unimportant to the bigger point, but for the purpose of this blog post I'll assume that each member state has to decide whether they will “spring forward” one last time on March 28th 2021, then staying in permanent “summer time”, or “fall back” one last time on October 31st 2021, then staying in permanent “winter time”. So from November 1st 2021 onwards, the UTC offset of each country will be fixed – but there may be countries which currently always have the same offset as each other, and will have different offsets from some point in 2021. (For example, France could use winter time and Germany could use summer time.)

The larger point is that time zone rules change, and that applications should expect that they will change. This isn't a corner case, it's the normal way things work. There are usually multiple sets of rule changes (as released by IANA) each year. At least in the European changes, we're likely to have a long notice period. That often isn't the case – sometimes we don't find out about rule changes until a few days before they happen.

Extra_End

wesdoyle followed 04/01/2024 Shay Rojansky roji, Principal software engineer working on .NET data access and perf, member of the Entity Framework team at Microsoft. Lead dev of Npgsql, the PostgreSQL provider.

When “UTC everywhere” isn't enough - storing time zones in PostgreSQL and SQL Server - Shay Rojansky's Blog (roji.org) 27/3/2019

When “UTC everywhere” isn't enough

I've been dealing a lot with timestamps, timezones and database recently - especially on PostgreSQL (see this blog post), but also in general. Recently, on the Entity Framework Core community standup, we also hosted Jon Skeet  and chatted about NodaTime, timestamps, time zones, UTC and how they all relate to databases - I highly recommend watching that!

Now, a lot has been said about “UTC everywhere”; according to this pattern, all date/time representations in your system should always be in UTC, and if you get a local timestamp externally (e.g. from a user), you convert it to UTC as early as possible. The idea is to quickly clear away all the icky timezone-related problems, and to have a UTC-only nirvana from that point on. While this works well for many cases - e.g. when you just want to record when something happened in the global timeline - it is not a silver bullet, and you should think carefully about it. Jon Skeet already explained this better than I could, so go read his  blog post on this. As a very short tl;dr, time zone conversion rules may change after the moment you perform the conversion, so the user-provided local timestamp (and time zone) may start converting to a different UTC timestamp at some point! As a result, for events which take place on a specific time in a specific time zone, it's better to store the local timestamp and the time zone (not offset!).

So let's continue Jon's blog post, and see how to actually perform that on two real databases - PostgreSQL and SQL Server. Following Jon's preferred option, we want to store the following in the database:

1. 1. The user-provided local timestamp.
2. 2. The user-provided time zone ID. This is not an offset, but rather a daylight savings-aware time zone, represented as a string.
3. 3. A UTC timestamp that's computed (or generated) from the above two values. This can be used to order the rows by their occurrence on the global timeline, and can even be indexed.

In Jon's  NodaTime library, the ZonedDateTime type precisely represents the first two values above. Unfortunately, databases typically don't have such a type; SQL Server does have datetimeoffset, but an offset is not a time zone (it isn't daylight savings-aware). So we must use separate columns to represent the data above.

PostgreSQL

PostgreSQL conveniently has a type called timestamp without time zone for local timestamps in an unspecified time zone, and a badly-named type called timestamp with time zone, for UTC timestamps (no time zone is actually persisted); those are perfect for our two timestamps. We also want the UTC timestamp to be generated from the two other values, so we’ll set up a PostgreSQL generated column (called computed column by EF Core) to do that. Here's the minimal EF Core model and context, using the NodaTime plugin:

Extra_End

Upgrade .NET version of XXX Server Components

To support TLS 1.2 capabilities, the recommendation to upgrade the app to .NET Framework 4.7 or a later version.

We only upgrade XXX Server components with .NET 4.7.2 and XXX Agent still on .NET 4.5.2

Technical Description

XXX Management Service, XXX Management Tool and Configuration Loader Component will be targeted to .NET 4.7.2 from 4.5.2

All associated Query/3rd party open source will be updated with the right version and the targeting framework.

For .NET Framework 3.5 - 4.5.2 and not WCF

We recommend you upgrade your app to .NET Framework 4.7 or a later version. If you cannot upgrade, take the following steps:

1. 1. Set the values of SchUseStrongCrypto and SystemDefaultTlsVersions registry entries to 1. See Configuring security via the Windows Registry..NET Framework 3.5 supports the SchUseStrongCrypto flag only when an explicit TLS value is passed.
2. 2. If you're running on .NET Framework 3.5, you need to install a hot patch so that TLS 1.2 can be specified by your program:

Extra_End

Enabling TLS 1.2 on your .NET application by Dominic Burford12/12/2019

I recently came across an issue with several of our ASP.NET WebAPI services which were consuming a third-party set of APIs. These third-party APIs were configured to disable any requests from clients that were using TLS 1.0/1.1. Unfortunately, this included our own APIs. All requests to the third-party API were returning empty responses. After some discussion with one of the developers of the third-party APIs, he suggested the issue may be related to TLS 1.2 not being supported as he had seen the issue before.

Claps: 25

- Transport Layer Security (TLS) best practices with the .NET Framework | Microsoft Docs

I was able to run the third-party APIs from our local test environment, but not when I ran them from our staging / production environments which were hosted on Azure. I had to make several changes, including code changes to the ASP.NET WebAPI services and changes to our Azure hosting environments.

As many current servers are moving towards TLS 1.2/1.3 and removing support for TLS 1.0 /1.1, connectivity issues between newer servers and older (legacy) .NET applications are becoming more common. Installing a newer version of the .NET Framework onto your development environment is not the answer. The solution is down to the version of the .NET Framework used for compiling your project. This is what actually matters when it comes to selecting the supported TLS version during the TLS handshake.

In this article I will describe the changes I have made to our Azure hosting (where our ASP.NET WebAPIs are hosted) and the code changes which enabled TLS 1.2 support.

Upgrading our Azure hosting to support TLS 1.2

More accurately the changes I have made to our Azure hosting have removed support for earlier versions of TLS i.e. TLS 1.0/1.1. Although this change was not strictly necessary to fix the problem I was experiencing, it was appropriate in terms of tightening up the security of our ASP.NET WebAPIs and to ensure that our own APIs can only be accessed by clients that support TLS 1.2. This is quite simply achieved by opening the Azure portal and navigating to the App Service hosting. From there the TLS/SSL Settings blade can be selected.

I have set this to TLS 1.2 for both our staging and production environments. This sets the minimum TLS version. Therefore our hosting environments will no longer accept requests from earlier versions of TLS.

Code changes to support TLS 1.2

Depending on what version of .NET Framework your project uses will dictate the possible solutions available to you. If your project compiles against .NET Framework >= 4.7 then you are already good to go. Applications developed in .NET Framework 4.7 or greater automatically default to whatever the operating system they run on considers safe (which currently is TLS 1.2 and will later include TLS 1.3).

If your application has been developed in a version of the .NET Framework prior to 4.7 then you have two options.

Recompile your application using .NET Framework 4.7 or greater - If recompiling your application is not something you can do then you can update your .config file by adding the following.

            <configuration>
              <runtime>
                <AppContextSwitchOverrides value="Switch.System.Net.DontEnableSystemDefaultTlsVersions=false"/>
              </runtime>
            </configuration>
            

Also make sure you have the following set in your .config file.

            <system.web>
              <compilation targetFramework="x.y.z" />
              <httpRuntime targetFramework="x.y.z" /> <-- this is the important one!
            </system.web>
            

Extra_End

Setting up ASP.NET Core dev certs for both WSL and Windows04/05/2021

For those of you who haven't read the old post, here is some background information. If you ever want to do your ASP.NET Core development using both WSL (using the Remote - WSL extension) and Windows, you will soon realize that there are some inherent issues with the local development certs… Mainly that ASP.NET Core sets up one development certificate in Windows, and one in Linux. And neither environment trusts the other. Not to mention that Linux doesn't even trust its own cert, making server to server communication hard in Linux.

Unfortunately, the tools provided by dotnet doesn't quite seem to do the trick when trying to get mutual trust to work. I'm not sure why, but at least on my machine, any cert that is generated by dotnet has problems when it comes to being able to trust it in Linux. So because of this, there are a few hoops we need to jump through to get this to work…

Note: My guess is that Linux requires a CA to issue the cert to be able to trust it. However, the cert generated by .NET is not a properly issued cert with a CA as this has some inherent dangers… Dangers I will ignore on my development box, and try to mitigate by keeping my cert VERY safe

In the previous post, there were quite a few steps involved in getting it to work. However, it can be simplified a bit at least…and made to work…

Dev certs in Linux

When you install the .NET SDK, an ASP.NET developer certificate is generated and configured for use by ASP.NET. However, it doesn't seem like that cert is being properly trusted by Linux, causing server to server communication to fail. Because of this, we need to generate our own self-signed cert. Luckily, this isn't too hard with the help of Google…

The first step is to create an OpenSSL configuration file that looks like this

            [req]
            prompt                  = no
            default_bits            = 2048
            distinguished_name      = subject
            req_extensions          = req_ext
            x509_extensions         = x509_ext
            [subject]
            commonName              = localhost
            [req_ext]
            basicConstraints        = critical, CA:true
            subjectAltName          = @alt_names
            [x509_ext]
            basicConstraints        = critical, CA:true
            keyUsage                = critical, keyCertSign, cRLSign, digitalSignature,keyEncipherment
            extendedKeyUsage        = critical, serverAuth
            subjectAltName          = critical, @alt_names
            1.3.6.1.4.1.311.84.1.1  = ASN1:UTF8String:ASP.NET Core HTTPS development certificate
            [alt_names]
            DNS.1                   = localhost
            DNS.2                   = 127.0.0.1
            

Note: This config creates a certificate that is both a CA and an SSL cert. The reason for this is that Linux needs a CA cert to be able to trust it.

Once we have our OpenSSL configuration, we can go ahead and generate our certificate by running

            > openssl req -x509 -nodes -days 365 -newkey rsa:2048 \
               -keyout localhost.key \
               -out localhost.crt \
               -config localhost.conf

This generates a key pair based on the configuration file we just created.

Just for the sake of it, we can verify that it currently isn't trusted, by running

            > openssl verify localhost.crt

            CN = localhost
            error 18 at 0 depth lookup: self signed certificate
            error localhost1.crt: verification failed

To trust the cert, we need to copy it to /usr/local/share/ca-certificates, and add it to our trusted CA:s. Like this

           > sudo cp localhost.crt /usr/local/share/ca-certificates
           > sudo update-ca-certificates

After that, we should be able to verify that the cert is trusted by running openssl verify again

            > openssl verify localhost.crt

            localhost.crt: OK

The last step is to make sure that ASP.NET Core uses this certificate when SSL is turned on. This is easily done by running the dotnet dev-certs command. However, this command expects a PKCS12 certificate. So before we can do that, we need to convert our key pair into a PKCS12 cert using OpenSSL

          openssl pkcs12 -export -out localhost.pfx -inkey localhost.key -in localhost.crt

Once we have out PFX-file, we can finally tell ASP.NET to use it by running

Remember: Make sure it is a secure password! If anyone should get their hands on this cert, it could be used to launch a malicious attack against your machine. So keeping it safe is VERY important! And also make sure that the key pair is stored in a safe place.

Ok, that's it from the Linux side…

Dev certs in Windows

When you install the .NET Core SDK on Windows, it creates a development HTTPS certificate for you automatically just like it does in Linux. All you have to do is run dotnet dev-certs https --trust to trust it and you are good to go! However, in this case we want to replace that cert with the cert we just created…

The first step in doing this, is to get hold of the PFX file we just generated. On my machine, I copy it to a user specific folder by running the following command in WSL

Author of Blog: Chris Klug

If you have any comments or questions, feel free to reach out at @ZeroKoll!

Extra_End

SEAF: A Scalable, Efficient, and Application-independent Framework for container security detection - ScienceDirect __/12/2022

Author links open overlay panelLibo Chen a, Yihang Xia b, Zhenbang Ma c, Ruijie Zhao a, Yanhao Wang c, Yue Liu d, Wenqi Sun a, Zhi Xue a

Citations: 6

Extra_End

wilsonmar (Wilson Mar) (github.com) followed @spotakash24/10/2021

Azure Cross Tenant Access (Authentication, Authorization, Private Communication).

There are two idependent Azure tenants, across which we shall try to build authentication, authorization. Subsequently, we shall have secure private connectivity between both tenant so that communication does not traverse through internet and remain private.

1. 1. Source Tenant: Tenant which is Central Identity Store. This identity store (Azure AD) will create and store Service Principals. In Source Tenant, We are processing data residing in Destination tenant.
2. 2. Destination Tenant: Tenant where data is coming in and residing. Data from this tenant can not move out. It is data store.

Note: Have understanding in Azure Active Diretory what is Application Registration, Enterprise Application (Service Pricipal)

Requirements:
1. 1. Systems, running in Source Tenant, should be able to reach Destination Tenant.
2. 2. While doing so, proper secured authentication and authorization should be performed.
3. 3. For authentication in Destination Tenant, no guest account access should be used.
4. 4. Request should not traverse through Internet and traffic should remain total private.
5. 5. Source and Destination tenant can not have any sort of Virtual Network Peering or Mesh Private Connectivity between them.
6. 6. All requests at Source Tenant and Destination on Identity, Connectivity and Data Layer should be logged in loganalytics for compliance purpose.
7. 7. No Private IP hardcoding should be used in any system. Proper FQDNs based DNS resolution happen while accessing/processing data.

Solution:
1. 1. Use Multi-tenant Azure AD Service Principal (Enterprise Application) to authenticate across Source and Destination Tenants.
2. 2. Use Cross Tenant Private Endpoint to access resources over Private Network (Microsoft Backbone Network), without having any Virtual Network Peering or Mesh Private Connectivity
3. 3. Centralized Azure Private DNS Zone for DNS Resoluation for Cross Tenant DNS resolution to Private Endpoint

Pre-Requirements:
1. 1. Source and Destination Tenant Administrative Rights to create Application under Application Registration
2. 2. Have a virtual network with subnet (ideally) to be used for Private Endpoint, in Source Tenant.
3. 3. Source and Destination Tenant Administratibe Rights to create cross tenant Private Endpoint Request (at Source Tenant) And Approval (at Destination Tenant)
4. 4. Sufficient IAM Role to assign IAM to Service Principal (created above) on Azure resource example: Storage/DB/Redis/AKS etc. (at Destination Tenant).
   1. 4a. Atleast, Azure Resource Manager Reader role
   2. 4b. For Storage Access (example), data access role, such as Storage Blob Data Contributor
   3. 4c. Define your IAM strategy accordingly. Treat both Control Plane and Data Plane permission Good Azure Document to Refer.

5. 5. If using existing Centralized Azure Private DNZ Zone (in our case we are using), atleast Private DNZ Zone Contributor to allow you to create DNS Record for Existing Private Endpoint

Technical Steps

1. 1. Have Service Principal in Source Tenant Identity Store (AAD)

   az ad sp create-for-rbac -n "cross-tenant-app"

2. 2. Retrieving and verifying details
   1. 2.1. Note down Application ID and Secret generated in Source Tenant
   2. 2.2. Verify Application ID Listed in Application Registration (as Application (client) ID) and 'Enteprise Application' (as Application ID).

3. 3. Go to Application Registration/Authentication and Enable for ApplicationID 'Accounts in any organizational directory (Any Azure AD directory - Multitenant)
4. 4. By doing these steps, a multi-tenant Service Principal has been created in Source Tenant.

Stars: 10

Extra_End

Sidecar Proxy Pattern - The Basis Of Service Mesh by Ivan Velichko

Sidecar Proxy Pattern - The Basis Of Service Mesh07/08/2021

Sidecar Proxy Pattern - The Basis Of Service Mesh by @iximiuz

Heart: 347

Author of Blog: Ivan Velichko

Learning Containers, Kubernetes, and Backend Development

Want to learn Docker or Kubernetes? Struggle to understand what this Cloud Native buzz is about? On a mission to master Server-Side Craft? Then you're at the right place!

• ✔  In-depth technical materials.
• ✔  Focus on true fundamentals.
• ✔  Clear and visual explanations.
• ✔  Interactive playgrounds.New

As someone going through a similar learning journey, I keep my articles experiential and put a great deal of effort into explanatory drawings and interactive playgrounds.

Most popular posts

• ⭐  How Kubernetes Reinvented Virtual Machines
• ⭐  Learning Containers From The Bottom Up
• ⭐  Containers vs. Pods - Taking a Deeper Look
• ⭐  Container Networking Is Simple!
• ⭐  Computer Networking Basics For Developers
• ⭐  A Visual Guide to SSH Tunnels
• ⭐  From Docker Container to Bootable Linux Disk Image
• ⭐  The Need For Slimmer Containers
• ⭐  DevOps, SRE, and Platform Engineering

Extra_End

Coda Hale codahale (github.com) followed @samuel-lucas6

Guidance on implementing cryptography as a developer by Samuel Lucas12/01/2023

Kryptor: A simple, modern, and secure encryption and signing tool.

Geralt: A modern cryptographic library for .NET based on libsodium and inspired by Monocypher.

Cahir: A deterministic password manager.

Milva: A simple, cross-platform command line tool for hashing files and text.

Vanity: A simple WireGuard vanity public key generator.

The AEGIS Family of Authenticated Encryption Algorithms: The AEGIS-128L, AEGIS-256, AEGIS-128X, and AEGIS-256X Internet-Draft.

Balloon Hashing: An Internet-Draft for the Balloon password hashing function.

Encrypt-then-MAC for Committing AEAD (cAEAD): An Internet-Draft and committing ChaCha20-BLAKE2b AEAD implementation.

Cryptography Guidelines: Guidance on implementing cryptography as a developer.

This document outlines recommendations for cryptographic algorithm choices and parameters as well as important implementation details based on what I have learnt from reading about the subject and the consensus I have observed online. Note that some knowledge of cryptography is required to understand the terminology used in these guidelines.

My goal with these guidelines is to provide a resource that I wish I had access to when I first started writing programs related to cryptography. If this information helps prevent even just one vulnerability, then I consider it time well spent.

Acknowledgements

These guidelines were inspired by this Cryptographic Best Practices gist, Latacora's Cryptographic Right Answers, and Crypto Gotchas, which is licensed under the Creative Commons Attribution 4.0 International License. The difference is that I mention newer algorithms and have tried to justify my algorithm recommendations whilst also offering important notes about using them correctly.

Disclaimer

I am a psychology undergraduate with an interest in applied cryptography, not an experienced cryptographer. I primarily have experience with the libsodium library since that's what I've used for my projects, but I've also reported some security vulnerabilities related to cryptography.

Most experienced cryptographers don't have the time to write things like this, and the following information is freely available online or in books, so whilst more experience would be beneficial, I'm trying my best to provide accurate information that can be fact checked. If I've made a mistake, please contact me to get it fixed.

Note that the rankings are based on my opinion, algorithm availability in cryptographic libraries, and which algorithms are typically used in modern protocols, such as TLS 1.3, Noise Protocol Framework, WireGuard, and so on. Such protocols and recommended practices make for the best guidelines because they have been approved by experienced professionals.

General Guidelines

1. Research, research, research: you often don't need to know how cryptographic algorithms work under the hood to implement them correctly, just like how you don't need to know how a car works to drive. However, you need to know enough about what you're trying to do, which requires looking up relevant information online or in books, reading the documentation for the cryptographic library you're using, reading RFC standards, reading helpful blog posts, and reading guidelines like this one. Furthermore, reading books about the subject in general will be beneficial, again like how knowing about cars can help if you break down. For a list of great resources, check out my How to Learn About Cryptography blog post.

2. Check and check again: it's your responsibility to get things right the first time around to the best of your ability rather than relying on peer review. Therefore, I strongly recommend always reading over security sensitive code at least twice and testing it to ensure that it's operating as expected (e.g. checking the value of variables line by line using a debugger, using test vectors, etc).

3. Peer review is great but often doesn't happen: unless your project is popular, you have a bug bounty program with cash rewards, or what you're developing is for an organisation, very few people, perhaps none, will look through the code to find and report vulnerabilities. Similarly, receiving funding for a code audit will probably be impossible.

4. Please don't create your own custom cryptographic algorithms (e.g. a custom cipher or hash function): this is like flying a Boeing 747 without a pilot license but worse because even experienced cryptographers design insecure algorithms, which is why cryptographic algorithms are thoroughly analysed by a large number of cryptanalysts, usually as part of a competition. By contrast, you rarely see experienced airline pilots crashing planes. The only exception to this rule is implementing something like Encrypt-then-MAC with secure, existing cryptographic algorithms when you know what you're doing.

5. Please avoid coding existing cryptographic algorithms yourself (e.g. coding AES yourself): cryptographic libraries provide access to these algorithms for you to prevent people from making mistakes that cause vulnerabilities and to offer good performance. Whilst a select few algorithms are relatively simple to implement, like HKDF, many aren't and require a great deal of experience to implement correctly. Lastly, another reason to avoid doing this is that it's not much fun since academic papers and reference implementations can be very difficult to understand.

Cryptographic Libraries

Use(In Order)

1. Libsodium: a modern, extremely fast, easy-to-use, well documented, and audited library that covers all common use cases, except for implementing TLS. However, it's much bigger than Monocypher, meaning it's harder to audit and not suitable for constrained environments, and requires the Visual C++ Redistributable to work on Windows.

2. Monocypher: another modern, easy-to-use, well documented, and audited library, but it's about half the speed of libsodium on desktops/servers, has no misuse resistant functions (e.g. like libsodium's secretstream() and secretbox()), only supports Argon2i for password hashing, allowing for insecure parameters (please see the Password Hashing/Password-Based Key Derivation Notes section), and offers no memory locking, random number generation, or convenience functions (e.g. Base64/hex encoding, padding, etc). However, it's compatible with libsodium whilst being much smaller, portable, and fast for constrained environments (e.g microcontrollers).

3. Tink: a misuse resistant library that prevents common pitfalls, like nonce reuse. However, it doesn't support hashing or password hashing, it's not available in as many programming languages as libsodium and Monocypher, the documentation is a bit harder to navigate, and it provides access to some algorithms that you shouldn't use.

4. LibHydrogen: a lightweight, easy-to-use, hard-to-misuse, and well documented library suitable for constrained environments. The downsides are that it's not compatible with libsodium whilst also running slower than Monocypher. However, it has some advantages over Monocypher, like support for random number generation, even on Arduino boards, and easy access to key exchange patterns, among other things.

Avoid(In Order)

1. A random library (e.g. with 0 stars) on GitHub: assuming it's not been written by an experienced professional and it's not a libsodium or Monocypher binding to another programming language, you should generally stay away from less popular, unaudited libraries. They are much more likely to suffer from vulnerabilities and be significantly slower than the more popular, audited libraries. Also, note that even experienced professionals make mistakes.

2. OpenSSL: very difficult to use, let alone use correctly, offers access to algorithms and functions that you shouldn't use, the documentation is a mess, and lots of vulnerabilities have been found over the years. These issues have led to OpenSSL forks and new, non-forked libraries that aim to be better alternatives if you need to implement TLS.

3. The library available in your programming language: most languages provide access to old algorithms (e.g. MD5 and SHA1) that shouldn't be used anymore instead of newer ones (e.g. BLAKE2, BLAKE3, and SHA3), which can lead to poor algorithm choices. Furthermore, the APIs are typically easy to misuse, the documentation may fail to mention important security related information, and the implementations will be slower than libsodium. However, certain languages, such as Go and Zig have impressive modern cryptography support.

4. Other popular libraries I haven't mentioned (e.g. BouncyCastle, CryptoJS, etc): these again often provide or rely on dated algorithms and typically have bad documentation. For instance, CryptoJS uses an insecure KDF called EVP_BytesToKey() in OpenSSL when you pass a string password to AES.encrypt(), and BouncyCastle has no C# documentation. However, this recommendation is too broad really since there are some libraries that I haven't mentioned that are worth using, like PASETO. Therefore, as a rule of thumb, if it doesn't include several of the algorithms I recommend in this document, then it's probably bad. Just do your research and assess the quality of the documentation. There's no excuse for poor documentation.

5. NaCl: an unmaintained, less modern, and more confusing version of libsodium and Monocypher. For example, crypto_sign() for digital signatures has been experimental for several years. It also doesn't have password hashing support and is difficult to install/package.

6. TweetNaCl: unmaintained, slower than Monocypher, doesn't offer access to newer algorithms, doesn't have password hashing, and does not zero out buffers.

Notes

1. If the library you're currently using/planning to use doesn't support several of the algorithms I'm recommending, then it's time to upgrade and take advantage of the improved security and performance benefits available to you if you switch.

2. Please read the documentation: don't immediately jump into coding something because that's how mistakes are made. Good libraries have high quality documentation that will explain potential security pitfalls and how to avoid them.

3. Some libraries release unauthenticated plaintext when using AEADs: for example, OpenSSL and BouncyCastle apparently do. Firstly, don't use these libraries for this reason and the reasons I've already listed. Secondly, never do anything with unauthenticated plaintext; ignore it to be safe.

4. Older doesn't mean better: you can argue that older algorithms are more battle tested and therefore proven to be a safe choice, but the reality is that most modern algorithms, like ChaCha20, BLAKE2, and Argon2, have been properly analysed at this point and shown to offer security and performance benefits over their older counterparts. Therefore, it doesn't make sense to stick to this overly cautious mindset of avoiding newer algorithms, except for algorithms that are still candidates in a competition (e.g. new post-quantum algorithms), which do need further analysis to be considered safe.

5. You should prioritise speed: this can make a noticeable difference for the user. For example, a C# Argon2 library is going to be significantly slower than Argon2 in libsodium, meaning unnecessary and unwanted extra delay during key derivation. Libsodium is the go-to for speed on desktops/servers, and Monocypher is the go-to for constrained environments (e.g. microcontrollers).

Stars: 395

Extra_End

Stars: 685

Author of Blog:Aaron Toponce

Cryptographic Best Practices

Extra_End

Connor Leechconnor11528 followed James Bradygoodgravy18/03/2021

About

Redirect ActiveRecord (Rails) reads to replica databases while ensuring all writes go to the primary database.

This is a slight modification of Rocket Job's original library, simply renaming it from active_record_slave to active_record_replica.

In order to more clearly distinguish the library from active_record_slave, we also incremented the major version – it is, however, functionally equivalent.

active_record_replica redirects all database reads to replica instances while ensuring that all writes go to the primary database. active_record_replica ensures that any reads that are performed within a database transaction are by default directed to the primary database to ensure data consistency.

Production Ready. Actively used in large production environments.

1. 1.1 Redirecting reads to a single replica database.
2. 1.2 Works with any database driver that works with ActiveRecord.
3. 2. Supports all Rails 3, 4, or 5 read apis.
   1. 2.1. Including dynamic finders, AREL, and ActiveRecord::Base.select.
   2. 2.2. NOTE: In Rails 3 and 4, QueryCache is only enabled for BaseConnection by default. In Rails 5, it's enabled for all connections. (PR)

4. 3. Transaction aware
   1. 3.1. Detects when a query is inside of a transaction and sends those reads to the primary by default.
   2. 3.2. Can be configured to send reads in a transaction to replica databases.

5. 4. Lightweight footprint.
6. 5. No overhead whatsoever when a replica is not configured.
7. 6. Negligible overhead when redirecting reads to the replica.
8. 7. Connection Pools to both databases are retained and maintained independently by ActiveRecord.
9. 8. The primary and replica databases do not have to be of the same type.
   1. 8.1. For example Oracle could be the primary with MySQL as the replica database.

10. 9. Debug logs include a prefix of Replica: to indicate which SQL statements are going to the replica database.

            # Read from the replica database
            r = Role.where(name: 'manager').first
            r.description = 'Manager'
            
            # Save changes back to the primary database
            r.save!
 
            Example showing how reads within a transaction go to the primary

            Role.transaction do
            r = Role.where(name: 'manager').first
            r.description = 'Manager'
            r.save!
            end
            

Stars: 160

Extra_End

RSA is deceptively simple (and fun)15/01/2024

While reading Real-World Cryptography, I came across the "million message attack". This is an attack that Daniel Bleichenbacher demonstrated in 1998, which effectively broke RSA with a particular encoding function called PKCS #1. It was only mentioned briefly, so I dug in and decided to try to understand the attack, eventually to implement it.

Most crypto libraries do not ship with a vulnerable implementation of this, for good reason. It's been broken! And if I implement the full attack against a real implementation, it would also come with using realistic key size.

Instead, I decided to implement RSA myself so that I could implement a weak encoding scheme so I could implement the Bleichenbacher attack! So far, I have an implementation of RSA and of PKCS (the vulnerable one). The basics of RSA took an hour to implement, then what felt like days to debug. And now it (seemingly) works! The attack will follow soon, with any luck.

What's RSA, anyway?

RSA is a public-key cryptosystem, in contrast to symmetric key cryptosystems. With symmetric keys, the sender and the recipient both share a key and use the same key to encrypt and decrypt the message. In contrast, public-key cryptosystems have a key pair, a public and a private key. The public key can be used to encrypt messages and the private key to decrypt them¹.

One of the drawbacks of a symmetric key system is that you have to share the key. This means you have to use a different secure channel to transmit the key, and then both parties need to be really careful to keep it a secret. This isn't manageable for a system with a lot of participants, like the internet!

But symmetric key encryption is often very fast, and we have some of the operations for it even baked into hardware. It would be nice to use it where we can for that efficiency.

In contrast, with public-key cryptography, you can freely share the public key, and anyone can then use that to encrypt a message to you. This means you do not need a separate secure channel to share the key! (Although this ignores the whole problem of validating that the key comes from the right person, so you're not having your connection spoofed by an interloper.) And this is great! This is what RSA gives us, but the computations for RSA are slow and the messages you can send are also small.

In practice, RSA was used (regrettably, sometimes still is) to establish a secure connection and perform a key exchange, and then the keys you exchange let you use symmetric key encryption. You probably shouldn't use RSA. Modern alternatives exist that are better, like Curve25519 and other forms of elliptic-curve cryptography.

But for worse, we run into RSA, and it's also a fun historical artifact! It's worth understanding in, and hey, implementing it is just plain fun.

The basics of RSA

RSA is a nicely elegant cryptosystem. Its security is based on the difficulty of factoring the product of large prime numbers, and in its purest form it has no known breaks².However, as mentioned above, depending on how data is encoded, particular uses of it can be broken.

The basic operations of it are straightforward to express. There are three components:

1. 1. Generating keys
2. 2. Encrypting and decrypting!
3. 3. Encoding messages

We'll go through each of those, starting with generating keys.

Generating your keys

First of all, what even is a key? We know that it's used to encrypt or decrypt a message, but what is inside it?

For RSA, a key comprises two numbers. One of these is called the exponent and one is the modulus. A key could be (exp=3, mod=3233), for example. It's really just this pair of numbers³.

The reason the pieces of it are called the exponent and modulus is because of how we use them! RSA relies onmodular arithmetic (like clock math, if you're not familiar). These are the exponents and modulus for the encryption or decryption operations which we'll see later.

To generate a key, you follow a short procedure.

1. 1. First, pick two prime numbers which we'll call p and q. Then we compute n = p * q.
2. 2. Compute a number t = lcm(p-1, q-1). This is the totient, and we use this as our modulus for generating the keys but then never again.
3. 3. Pick the public exponent, which we'll call e. The requirement is that it shares no factors with t and is greater than 2. One simple way is to start with 3, but go up through the primes until you find one coprime with t. Choosing 65537 is also quite common, since it's small enough to be efficient for encryption but large enough to avoid some particular attacks.
4. 4. Calculate the private exponent, which we'll call d. We compute this as d = e^-1 mod t, or the inverse of e in our modulus.

Now you haved and e, the private and public exponents, and you have n, the modulus. Bundle those up into two tuples and you have your keys!

Let's work an example quickly to see how it ends up. For our primes, we can choose p = 17 and q = 29. So then n = 493.

Now we find t = lcm(17 - 1, 29 - 1) = lcm(16, 28) = 112 . We'll choose e = 3, which works since 2 < 3 and gcd(3, 112) = 1 so we know they share no factors. Now we compute ₄ d = e^-1 = 3^-1 = 75 mod 112. And then we have our keys!

Our public key is (exp=3, mod=493), and our private key is (exp=75, mod=493). We'll use these again in our examples on encrypting and decrypting!

Extra_End

Welcome to Lil'Log GitHub Link

Hi, this is Lilian. I'm documenting my learning notes in this blog. Besides, I'm leading a team working on practical AI safety and alignment at OpenAI. Based on the number of grammar mistakes in my posts, you can tell how much ChatGPT is involved 😉.

Author of Blog:Lilian

Followers on GitHub: 7k

Other Blog Posts by the Author

• 4. Some Math behind Neural Tangent Kernel8/09/2022

  Neural networks are well known to be over-parameterized and can often easily fit data with near-zero training loss with decent generalization performance on test dataset. Although all these parameters are initialized at random, the optimization process can consistently lead to similarly good outcomes. And this is true even when the number of model parameters exceeds the number of training data points.

• 3. Learning Word Embedding15/10/2017

• 2. Predict Stock Prices Using RNN: Part 222/07/2017

  Link to GitHub: lilianweng/stock-rnn

  Stars: 1.7k

  Predict stock market prices using RNN

1. Predict Stock Prices Using RNN: Part 18/07/2017

This is a tutorial for how to build a recurrent neural network using Tensorflow to predict stock market prices. The full working code is available in github.com/lilianweng/stock-rnn. If you don’t know what is recurrent neural network or LSTM cell, feel free to check my previous post.

One thing I would like to emphasize that because my motivation for writing this post is more on demonstrating how to build and train an RNN model in Tensorflow and less on solve the stock prediction problem, I didn’t try hard on improving the prediction outcomes. You are more than welcome to take my code as a reference point and add more stock prediction related ideas to improve it. Enjoy!

Predict stock market prices using RNN

One thing I would like to emphasize that because my motivation is more on demonstrating how to build and train an RNN model in Tensorflow and less on solve the stock prediction problem, I didn't try too hard on improving the prediction outcomes. You are more than welcome to take this repo as a reference point and add more stock prediction related ideas to improve it. Enjoy.

Check my blog post "Predict Stock Prices Using RNN": Part 1 and Part 2 for the tutorial associated.

1. 1. Make sure tensorflow has been installed.

2. 2. First download the full S&P 500 data from Yahoo! Finance ^GSPC (click the "Historical Data" tab and select the max time period). And save the .csv file to data/SP500.csv.

3. 3. Run python data_fetcher.py to download the prices of individual stocks in S & P 500, each saved to data/{ { stock_abbreviation.csv } }. (NOTE: Google Finance API returns the prices for 4000 days maximum. If you are curious about the data in even early times, try modify data_fetcher.py code to send multiple queries for one stock. Here is the data archive (stock-data-lilianweng.tar.gz) of stock prices I crawled up to Jul, 2017. Please untar this file to replace the "data" folder in the repo for test runs.)

4. 4. Run python main.py --help to check the available command line args.

5. 5. Run python main.py to train the model.

For examples,

• Train a model only on SP500.csv; no embedding

python main.py --stock_symbol=SP500 --train --input_size=1 --lstm_size=128 --max_epoch=50

Extra_End

Analyzing Data 180,000x Faster with Rust20/10/2023

This note documents one of my recent adventures in performance optimization with Rust. By following along, hopefully you'll learn something about how to write fast Rust.

Here's the context: imagine you have data from an online exam where a set of users answered a set of questions. The raw data looks like this:

           [
            {
              "user": "5ea2c2e3-4dc8-4a5a-93ec-18d3d9197374",
              "question": "7d42b17d-77ff-4e0a-9a4d-354ddd7bbc57",
              "score": 1
            },
            {
              "user": "b7746016-fdbf-4f8a-9f84-05fde7b9c07a",
              "question": "7d42b17d-77ff-4e0a-9a4d-354ddd7bbc57",
              "score": 0
            },  
            /* ... more data ... */
           ]


            PsuedoCode: 
            func k_corrset($data, $k):
                $all_qs = all questions in $data
                for all $k-sized subsets $qs within $all_qs:
                    $us = all users that answered every question in $qs
                    $qs_totals = the total score on $qs of each user in $us
                    $grand_totals = the grand score on $all_qs of each user in $us
                    $r = correlation($qs_totals, $grand_totals)
                return $qs with maximum $r  

            Python Baseline:

                from itertools import combinations
                import pandas as pd
                from pandas import IndexSlice as islice
                
                def k_corrset(data, K):
                    all_qs = data.question.unique()
                    q_to_score = data.set_index(['question', 'user'])
                    all_grand_totals = data.groupby('user').score.sum().rename('grand_total')
                
                    corrs = []
                    for qs in combinations(all_qs, K):
                        qs_data = q_to_score.loc[islice[qs,:],:].swaplevel()
                        answered_all = qs_data.groupby(level=[0]).size() == K
                        answered_all = answered_all[answered_all].index
                        qs_totals = qs_data.loc[islice[answered_all,:]] /
                            .groupby(level=[0]).sum().rename(columns={'score': 'qs'})
                        r = qs_totals.join(all_grand_totals).corr().qs.grand_total
                        corrs.append({'qs': qs, 'r': r})
                    corrs = pd.DataFrame(corrs)
                
                    return corrs.sort_values('r', ascending=False).iloc[0].qs
                
                data = pd.read_json('scores.json')
                print(k_corrset(data, K=5))

            

Note that each user only answered a subset of all possible questions, and all scores are either 0 or 1.

Here's the problem: given a size k, which set of k questions has the highest correlation with overall performance? We'll call this the k-CorrSet problem. A simple brute-force algorithm for solving the k-CorrSet problem looks like this pseudocode:

We are going to implement several variations on this algorithm to see how fast we can make it.

Can you explain in depth on this?

The algorithm iterates through all possible k-sized subsets of questions, calculates the correlation between the scores on that subset and the grand scores on all questions, and returns the subset with the maximum correlation.

ChatGPT:

Certainly! Let's break down the key steps of the algorithm that iterates through all possible k-sized subsets of questions, calculates the correlation, and returns the subset with the maximum correlation.

Here's a more detailed explanation:

1. 1. Generate all k-sized subsets of questions:

   The algorithm starts by obtaining all possible questions from the given dataset. Then, it iterates through all k-sized subsets of these questions. For example, if k is 3, it would consider all possible combinations of 3 questions out of the total set of questions.

2. 2. Identify users who answered every question in the subset:

   For each k-sized subset of questions, the algorithm identifies all users who answered every question in that subset. This is important because the correlation calculation requires data from users who answered all questions in the subset.

3. 3. Calculate total scores on the subset for each user:

   Once the algorithm has the subset of questions and the corresponding users, it calculates the total score on that subset for each user. It sums up the scores of each user for the questions in the subset.

4. 4. Calculate the grand total scores on all questions for each user:

   Simultaneously, the algorithm calculates the grand total scores on all questions for each user. This involves summing up the scores of each user for all questions, not just the subset.

5. 5. Calculate the correlation between subset scores and grand total scores:

   With the total scores on the subset and the grand total scores for each user, the algorithm calculates the correlation between these two sets of scores. The correlation coefficient is a measure of the linear relationship between two sets of data. It ranges from -1 to 1, where -1 indicates a perfect negative correlation, 1 indicates a perfect positive correlation, and 0 indicates no correlation.

   The correlation calculation could use statistical methods such as Pearson correlation coefficient, which measures the linear correlation between two variables. The formula for Pearson correlation is:

   𝑟 = ∑ (𝑥𝑖 − 𝑥¯)(𝑦𝑖 − 𝑦¯ ) / √ ∑ (𝑥𝑖 − 𝑥¯ )^2 ∑ (𝑦 − 𝑦¯ )^2

   Where:

   𝑥𝑖xi and 𝑦𝑖yi are the individual scores of the users on the subset and grand total, respectively.

   𝑥¯xˉ and 𝑦¯yˉ are the means of the scores on the subset and grand total, respectively.

6. 6. Return the subset with the maximum correlation:

   After calculating the correlation for each k-sized subset, the algorithm identifies the subset with the maximum correlation coefficient and returns it as the result. This subset is considered to have the highest correlation with overall performance.

Note:

The described algorithm is a brute-force approach, meaning it considers all possible subsets and calculates correlations for each. While it provides a straightforward solution to the k-CorrSet problem, it might be computationally expensive for large datasets. The author's exploration in Rust likely involves optimizing this algorithm or exploring alternative approaches to improve its efficiency.

Stars: 42

Link to the article:

Analyzing Data 180,000x Faster with Rust

Extra_End

osanseviero followed Christopher Fleetwood10/07/2021

I am a Machine Learning Engineer at HuggingFace in London, UK.

An exploration of fMRI timeseries similarity metrics

In order to perform classification on a functional brain scan it first undergoes many preprocessing steps. One of these steps is the transformation from the timeseries output of the fMRI scan, transforming a 𝑚 × 𝑛 m×n (where 𝑚 m is the number of timepoints recorded and 𝑛 n is the number of brain regions used) to an 𝑛 × 𝑛 n×n matrix of similiarity values (called a connectome). This similarity value is a measure of the neural synchronization between the 2 regions.

So how do we quantify the similarity of 2 different timeseries? This blog post will explore the common ways of quantifying time series similarity in a neuroscientific setting. Before we get into the actual methods used to calculate time series similarity, we need to cover the corner stone of almost all of the methods we are about to explore - covariance.

Covariance

Covariance is simply a measure of how two random variables change together. Below is the formula for calculating covariance:

Σ=E[(X−E[X])(X−E[X]) T ]

In the case of fMRI, we have a multivariate random variable, allowing us to use Maximum Likelihood Estimation to estimate the covariance matrix. Below is a toy example of our estimated covariance matrix.

• 1. Covariance is bound between − ∞ −∞ and ∞ ∞ making it less suitable for downstream classifiers.

• 2. Covariance coefficients are not standardized and cannot be used to quantify the strength of the relationship.

3. Symmetric Positive semi-definite (SPD) matricies do not naturally form a Euclidean space (this will be important later).

• 4. When the number of features is large relative to the number of observations, the sample/empirical covariance matrix has excessive estimation error.

Many of the following approaches will aim to address some or all of the above drawbacks with empirical covariance.

To address the excessive estimation error, it is common to perform a transformation to the covariance coefficients, known as "shrinkage". In their seminal paper, "Honey, I shrunk the Sample Covariance Matrix" [1], Ledoit & Wolf proposed using shrinkage to regularize the sample covariance matrix. "Shrinkage" as the name implies, pulls the most extreme covariance coefficients towards more central values. This not only resolves our excessive estimation error, it can also make the matrix easily invertable by encouraging numerical stability. (The interested reader should consult the scikit-learn docs [2] )

Now that we have a well conditioned covariance matrix, we can attempt to address some of the other identified drawbacks.

Canonical Approaches

Pearson's correlation coefficient (Pearson's 𝑅 R) or simply correlation, is the most commonly used method to quantify similarity between 2 fMRI timeseries. Correlation is a linear metric computed from the covariance of the 2 timeseries. Below is the mathematical formula to compute correlation for a pair of random variables:

Correlation is widely used in neuroscience as it has long statistical history and is bound between -1 and 1. However, correlation does have some disadvantages. The below figure should demonstrate one clearly:

Due to correlations linear nature, the same timeseries being slightly out of phase causes a huge decrease in the correlation value. Additionally, correlation provides no distinction between whether 2 regions are directly connected or indirectly connected via another region. To account for this, we can use partial correlation!

Partial correlation is a variant of PCC that attempts to address distinguishing between direct and indirect connections. This is done by computing correlation between regions after regressing all other timeseries. Partial correlation is computed from the inverse of the covariance matrix (this is where the shrinkage comes in handy), also known as the precision matrix. Below is the mathematical formula for computing partial correlation for a pair of random variables:

Author of Blog:Chris

Other Blog Posts by the Author

• 1. Layer Normalization as fast as possible. Details: One pass algorithm, Two-pass algorithm, Welford's algorithm, and Implementing Welford's Algorithm11/12/2023

• 2. Running LLMs with Browser in Rust26/04/2023

3. Rust based ML model analyzer18/10/2022

• 4. An exploration of fMRI timeseries similarity metrics10/07/2021

Extra_End

Author: Tim Dettmers

Understanding Convolution in Deep Learning26/03/2015

There are already some blog post regarding convolution in deep learning, but I found all of them highly confusing with unnecessary mathematical details that do not further the understanding in any meaningful way. This blog post will also have many mathematical details, but I will approach them from a conceptual point of view where I represent the underlying mathematics with images everybody should be able to understand. The first part of this blog post is aimed at anybody who wants to understand the general concept of convolution and convolutional nets in deep learning. The second part of this blog post includes advanced concepts and is aimed to further and enhance the understanding of convolution for deep learning researchers and specialists.

What is convolution?

You can imagine convolution as the mixing of information. Imagine two buckets full of information which are poured into one single bucket and then mixed according to a specific rule. Each bucket of information has its own recipe, which describes how the information in one bucket mixes with the other. So convolution is an orderly procedure where two sources of information are intertwined.

Convolution can also be described mathematically, in fact, it is a mathematical operation like addition, multiplication or a derivative, and while this operation is complex in itself, it can be very useful to simplify even more complex equations. Convolutions are heavily used in physics and engineering to simplify such complex equations and in the second part — after a short mathematical development of convolution — we will relate and integrate ideas between these fields of science and deep learning to gain a deeper understanding of convolution. But for now we will look at convolution from a practical perspective.

How do we apply convolution to images?

When we apply convolution to images, we apply it in two dimensions — that is the width and height of the image. We mix two buckets of information: The first bucket is the input image, which has a total of three matrices of pixels — one matrix each for the red, blue and green color channels; a pixel consists of an integer value between 0 and 255 in each color channel. The second bucket is the convolution kernel, a single matrix of floating point numbers where the pattern and the size of the numbers can be thought of as a recipe for how to intertwine the input image with the kernel in the convolution operation. The output of the kernel is the altered image which is often called a feature map in deep learning. There will be one feature map for every color channel.

Convolution of an image with an edge detector convolution kernel. Sources:

We now perform the actual intertwining of these two pieces of information through convolution. One way to apply convolution is to take an image patch from the input image of the size of the kernel — here we have a 100×100 image, and a 3×3 kernel, so we would take 3×3 patches — and then do an element wise multiplication with the image patch and convolution kernel. The sum of this multiplication then results in one pixel of the feature map. After one pixel of the feature map has been computed, the center of the image patch extractor slides one pixel into another direction, and repeats this computation. The computation ends when all pixels of the feature map have been computed this way. This procedure is illustrated for one image patch in the following gif.

As you can see there is also a normalization procedure where the output value is normalized by the size of the kernel (9); this is to ensure that the total intensity of the picture and the feature map stays the same.

Extra_End

One interesting Blog Post by the Author: Brandon Amos, Research Scientist, Meta, AI (FAIR), bda@meta.com

Image Completion with Deep Learning in TensorFlow09/08/2016

Content-aware fill is a powerful tool designers and photographers use to fill in unwanted or missing parts of images. Image completion and inpainting are closely related technologies used to fill in missing or corrupted parts of images. There are many ways to do content-aware fill, image completion, and inpainting. In this blog post, I present Raymond Yeh and Chen Chen et al.s paper “Semantic Image Inpainting with Perceptual and Contextual Losses,” which was just posted on arXiv on July 26, 2016. This paper shows how to use deep learning for image completion with a DCGAN. This blog post is meant for a general technical audience with some deeper portions for people with a machine learning background. I've added [ML-Heavy] tags to sections to indicate that the section can be skipped if you don't want too many details. We will only look at the constrained case of completing missing pixels from images of faces. I have released all of the TensorFlowsource code behind this post on GitHub atbamos/dcgan-completion.tensorflow.

1. We'll first interpret images as being samples from a probability distribution.
2. This interpretation lets us learn how to generate fake images.
3. Then we'll find the best fake image for completion.

Step 1: Interpreting images as samples from a probability distribution

How would you fill in the missing information?

In the examples above, imagine you're building a system to fill in the missing pieces.How would you do it? How do you think the human brain does it? What kind of information would you use?

In this post we will focus on two types of information:

1. Contextual information: You can infer what missing pixels are based on information provided by surrounding pixels.
2. Perceptual information: You interpret the filled in portions as being “normal,” like from what you've seen in real life or from other pictures.

Both of these are important. Without contextual information, how do you know what to fill in? Without perceptual information, there are many valid completions for a context. Something that looks “normal” to a machine learning system might not look normal to humans.

It would be nice to have an exact, intuitive algorithm that captures both of these properties that says step-by-step how to complete an image. Creating such an algorithm may be possible for specific cases, but in general, nobody knows how. Today's best approaches use statistics and machine learning to learn an approximate technique.

But where does statistics fit in? These are images.

To motivate the problem, let's start by looking at a probability distribution that is well-understood and can be represented concisely in closed form: a normal distribution. Here's the probability density function (PDF) for a normal distribution. You can interpret the PDF as going over the input space horizontally with the vertical axis showing the probability that some value occurs. (If you're interested, the code to create these plots is available at bamos/dcgan-completion.tensorflow:simple-distributions.py.)

Let's sample from the distribution to get some data. Make sure you understand the connection between the PDF and the samples.

[ML-Heavy] Generative Adversarial Net (GAN) building blocks

These ideas started with Ian Goodfellow et al.'s landmark paper “Generative Adversarial Nets” (GANs), published at the Neural Information Processing Systems (NIPS)conference in 2014. The idea is that we define a simple, well-known distribution and represent it as For the rest of this post, well use ... as a uniform distribution between -1 and 1 (inclusively). We represent sampling a number from this distribution as ... line of Python with numpy:

z = np.random.uniform(-1, 1, 5)array([ 0.77356483,  0.95258473, -0.18345086,  0.69224724, -0.34718733])

z = np.random.uniform(-1, 1, 5)
            array([ 0.77356483,  0.95258473, -0.18345086,  0.69224724, -0.34718733])

Next, suppose that you have a 3x3 input. Our goal is to upsample so that the output is larger. You can interpret a fractionally-strided convolution as expanding the pixels so that there are zeros in-between the pixels. Then the convolution over this expanded space will result in a larger output space. Here, it's 5x5.

Extra_End

One interesting Blog Post by the Author: PHILSCHMID

Getting started with CNNs by calculating LeNet-Layer manually28/02/2020

The idea of CNNs is intelligently adapt to the properties of images by reducing the dimension. To achieve this convolutional layer and pooling layer are used. Convolutional layers are reducing the dimensions by adding filters (kernel windows) to the Input. The dimension can reduce by applying kernel windows to calculate new outputs. Assuming the input shape is 'expression' and the kernel window ist 'expression' then the output shape will be.

Pooling Layers are reducing the dimension by aggregating the input elements. Assuming the input shape is 'expression' and the pooling method is average with a kernel window of 'expression' then the output shape will be

Example CNNs Architecture LeNet-5

This is the architecture of LeNet-5 created by Yann LeCun in 1998 and widely used for written digits recognition (MNIST).

To understand what is happening in each layer we have to clarify a few basics. Let's start with Stride and Padding

You can define padding as adding extra pixels as filler around the original input to decrease the erasion of information.

Example of adding p (1x1) to an input. If we add padding to our input the formula for calculating the output changes to

Extra_End

Sylvain Gugger GitHub: 3.2k Followers

A Neural Net In Pytorch16/03/2018

Archives

Thu 03 May 2018

Deep Painterly Harmonization

Thu 26 April 2018

Pointer cache for Language Model

Sat 14 April 2018

Recurrent Neural Network

Sat 07 April 2018

The 1cycle policy

Thu 05 April 2018

Convolution in depth

Thu 29 March 2018

SGD Variants

Tue 20 March 2018

A simple neural net in numpy

Tue 20 March 2018

How Do You Find A Good Learning Rate

Fri 16 March 2018

A Neural Net In Pytorch

Tue 13 March 2018

What Is Deep Learning?

Mon 12 March 2018

Why Write A Blog?

MNIST Dataset

To have some data on which try our neural net, we will use the MNIST Dataset. It's a set of hand-written digits that contains 70,000 pictures with their labels. It's divided in two parts, one training set with 60,000 digits (on which we will train our model) and 10,000 others that form the test. These were drawn by different people from the ones in the first test, and by evaluating how well on this set, we will see how well it actually generalizes what it learned.

We'll skip the part as to how to get those sets and how to treat them since it's all shown in the notebook. Let's go to the part where we define our neural net instead. The pictures we are given have a size of 28 by 28 pixels, each pixel having a value of 0 (white) to 1 (black), so that makes 784 inputs. For this simple model, we choose one hidden layer of 100 neurons, and then an output size of 10 since we have ten different digits.

Why 10 and not 1? It's true that in this case we could have asked for just one output going from 0 to 9 (and there are ways to make sure itt'd behave like this) but in image classification problems, we often give as many outputs as they are classes to determine. What if our next problem is to say if the picture if of a dog, a cat, a frog or a horse? One output wont't really represent this, whereas four outputs will certainly help, each of them representing the probability itt's in a given class.

Softmax

When we have a classification problem and a neural network trying to solve it with

If

Convolution in depthThu 29 March 2018

Convolution in depth

Since AlexNet won the ImageNet competition in 2012, linear layers have been progressively replaced by convolutional ones in neural networks trained to perform a task related to image recognition. Let's see what those layers do and how to implement them from scratch.

What is convolution?

The idea behind convolution is the use of image kernels. A kernel is a small matrix (usually of size 3 by 3) used to apply effect to an image (like sharpening, blurring...). This is best shown on this super cool page where you can actually see the direct effect on any image you like.

The core idea is that an image is just a bunch of numbers. Its representation in a computer is an array of size width by heights pixels, and each pixel is associated to three float values ranging from 0 to 1 (or integers going from 0 to 255). This three numbers represent the red-ness, green-ness and blue-ness of said pixel, the combination of the three capturing its color. A fourth channel can be added to represent the transparency of the pixel but we won't focus on that.

If the image is black and white, a single value can be use per pixel, with 0 meaning black and 1 (or 255) meaning white. Let's begin with this for the explanation. The convolution of our image by a given kernel of a given size is obtained by putting the kernel in front of every area of the picture, like a sliding window, to then do the element-wise product of the numbers in our kernel by the ones in the picture it overlaps and summing all of these, like in this picture:

Then we repeat the process by moving the kernel on every possible area of the picture.

As shown on this page mentioned earlier, by doing this on all the areas of our picture, sliding the kernel in all the possible positions, it will give another array of number that we can also interpret as a picture, and depending on the values inside of our kernel, this will apply different effects on the original image. The process is shown on this video

The idea behind a convolutional layer in a neural net is then to initialize the weights of kernels like the one we just saw at random, then use SGD to find the best possible parameters. It's possible to do this since the operation we are doing withour sliding window looks like

By stacking several convolutional layers one on top of the other, the hope is to get a neural network that captures the information we want on our image.

Extra_End

https://amaarora.github.io/ Aman Arora

Adam and friends

Adam, SGD, RMSProp from scratch in PyTorch.13/03/2021

4.1 What is Stochastic Gradient Descent?

For an intuitive understanding, refer fig-2 below:

Let's say we are standing at a certain point A of a parabolic hill as shown in fig-2 and we wish to find the lowest point on this curve. Can you think of some ways to do this? Well, we could try going in a random direction, calculate the value of the function and if it's lower than the previous value, we could take a step in that direction. But this process is slow. With some mathematical magic, we can make this process faster. In fact, the fastest way down a function or the steepest way down the hill is the one in the opposite direction of the gradient. Gradient at point A is the slope of the parabolic function, and by calculating the gradients, we can find the steepest direction in which to move to minimize the value of the function. This is referred to as Gradient Descent. Of course in a high dimensional space, calculating the gradients is a little bit more complicated than in fig-2 but the idea remains the same. We take a step from point A directed by the gradients to follow the steepest path downwards to point B to find the lowest value of the curve. The step-size is governed by a parameter called learning rate. The new position B then can be defined as B = A - lr * A.grad where A.grad represents the slope/gradients of the curve at point A.

The stochasticity in Stochastic Gradient Descent arises when we compute the batch gradients. This has been explained below through pseudo-code in Vanilla Stochastic Gradient Descent.

From the Introduction to SGD by Jeremy Howard, and from fig-2, we already know that to perform Gradient Descent, we need to be able to calculate the gradients of some function that we wish to minimise with respect to the parameters.

We don't need to manually calculate the gradients and as mentioned in this video by Jeremy, PyTorch can already do this for us using torch.autorgrad.

So now that we know that we can compute the gradients, the procedure of repeatedly evaluating the gradient and then performing a parameter update is called Gradient Descent. Its vanilla version looks as follows:

Extra_End

Zach Mueller GitHub Link

Hi! My name is Zachary Mueller, and I'm a Machine Learning Software Engineer at 🤗. I majored in Software Design and Development and I have minors in both Computer Science and Environmental Science.

I have a heavy passion for Deep Learning and Open Source libraries. As a result, below you will find some notable articles I've written, a few courses I've made, some of software libraries I've written, interesting projects, and the open source libraries I have tried to contribute the most to.

Author of Blog:Zach Mueller

Followers on GitHub: 1.2k

Other Blog Posts by the Author

1. Summer Smackdown - Week 17/07/2019

These posts will most likely wind up being a bit of an odd bunch in terms of formatting until I figure out a style I like and enjoy, as the goal is to merge all Four of the lessons into one big post.

Given I wanted to update all of these blogs on Sundays, I decided I would include the first ‘day’ of work as well.

Overall how the schedule I plan to follow looks is as such:

• M: Linear Algebra
• T: NLP, Matrix Calculus
• Th: Foundations, Matrix Calculus, Linear Algebra
• F: Foundations, NLP
• Sa: NLP, Linear Algebra, Matrix Calc, Foundations

As I started this goal on a Saturday, this week there will not be much in my recap, but I’ll be as inclusive as I can into the small lessons I learned.

Computational Linear Algebra

We start off learning about the Markov Chain, a way to describe a sequence of events where the probably of each event depends on the state of the previous event. Also known as the next event is determined by the previous event. The course utilizes the Numpy library to hold matrix multiplications to solve the various problems. My notes go through and futher explain what each answer means in context.

For example, problem 1 is about using a stochastic matrix, which is a square probablity matrix, in order to predict how health-related incidents will be in the following year.

We start off knowing that the current year had 85% asymtpmatic, 10% symptomatic, 5% AIDS, and 0% death. Next, we were given the following probability table:



Now that we’re here, we use matrix multiplication to get our answer:

    import numpy as np

    i = np.array([[.85,.1,.05,0]])
    mat = np.array([[.9,.07,.02,.01],
                    [0,.93,.05,.02],
                    [0,0,.85,.15],
                    [0,0,0,1]])
    
    res = mat.T @ i.T
    

• The @ symbol is used when doing matrix multiplication, where we multiply each row by the column, and then sum them together.

One thing Jeremy points out is another way to write the above:

(i @ mat).T) which saves us a few seconds of code, and looks cleaner.

The answer winds up being:

    array([[0.765 ],
        [0.1525],
        [0.0645],
        [0.018 ]])
    

However, what does the answer mean? Well, it means that within the next year:

• 76.5% of people will be asymptomatic
• 15.25% of people will be symptomatic
• 6.45% of people will have AIDS
• 1.8% of people will die as a result of their illnesses

We’ve started using some matrix multiplication to get solutions, but can we get a bit more advanced with it?

Take problem 2:



Given the above table, figure out which store is best for what individual. This is a straight matrix by matrix multiplication problem where we will have ‘dem’ represent a matrix of the demand per individual, and ‘p’ be the prices for each item in two particular shops.

    dem = np.array([[6, 5, 3, 1],
        [3,6,2,2],
        [3,4,3,1]])
 
 p = np.array([[1.5, 1],
        [2., 2.5],
        [5., 4.5],
        [16., 17.]])
    

We yet again solve this by doing dem@p, which gives us a table that looks like the following:

    array([[50. , 49. ],
        [58.5, 61. ],
        [43.5, 43.5]])
    

The above table is now described as having the rows be an individual, and the columns being a particular store with the content as the price they would pay for the items they need. We can see that for Person 1 shop 2 would be the best, for Person 2 shop 1 would be the best, and for Person 3 they could go to either one.

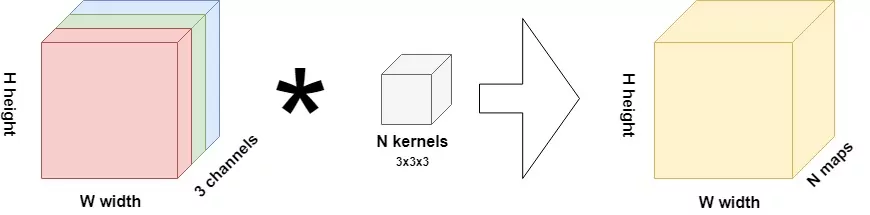
Then Rachel goes further to describe images a little bit and convolutions, which I was already familar with from the Practical Deep Learning for Coders course, however this Medium article she mentions I found especially helpful: CNNs from Different Viewpoints

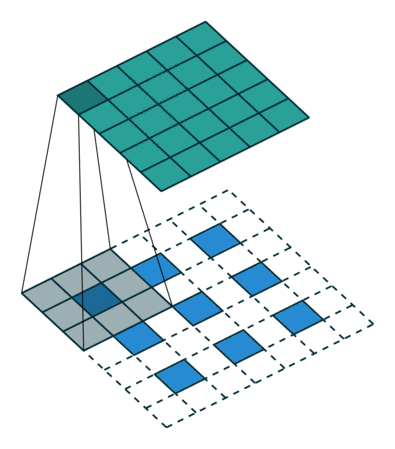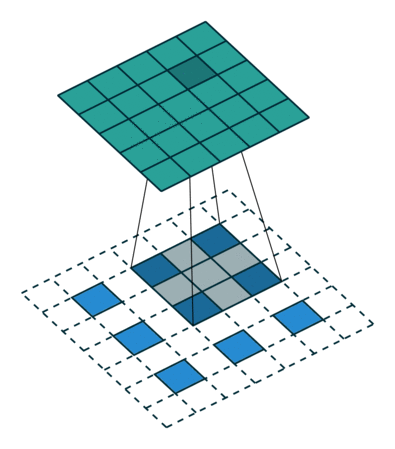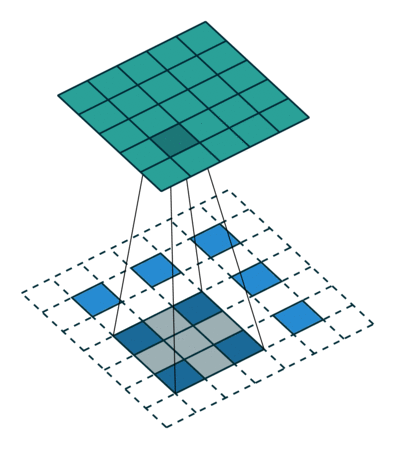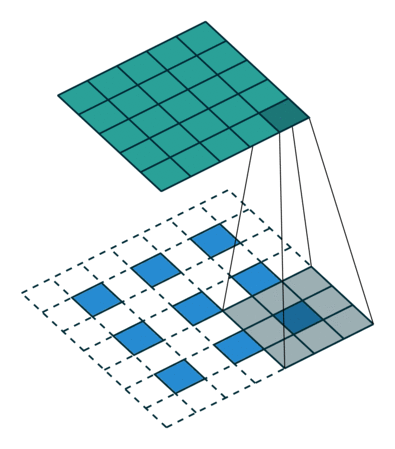
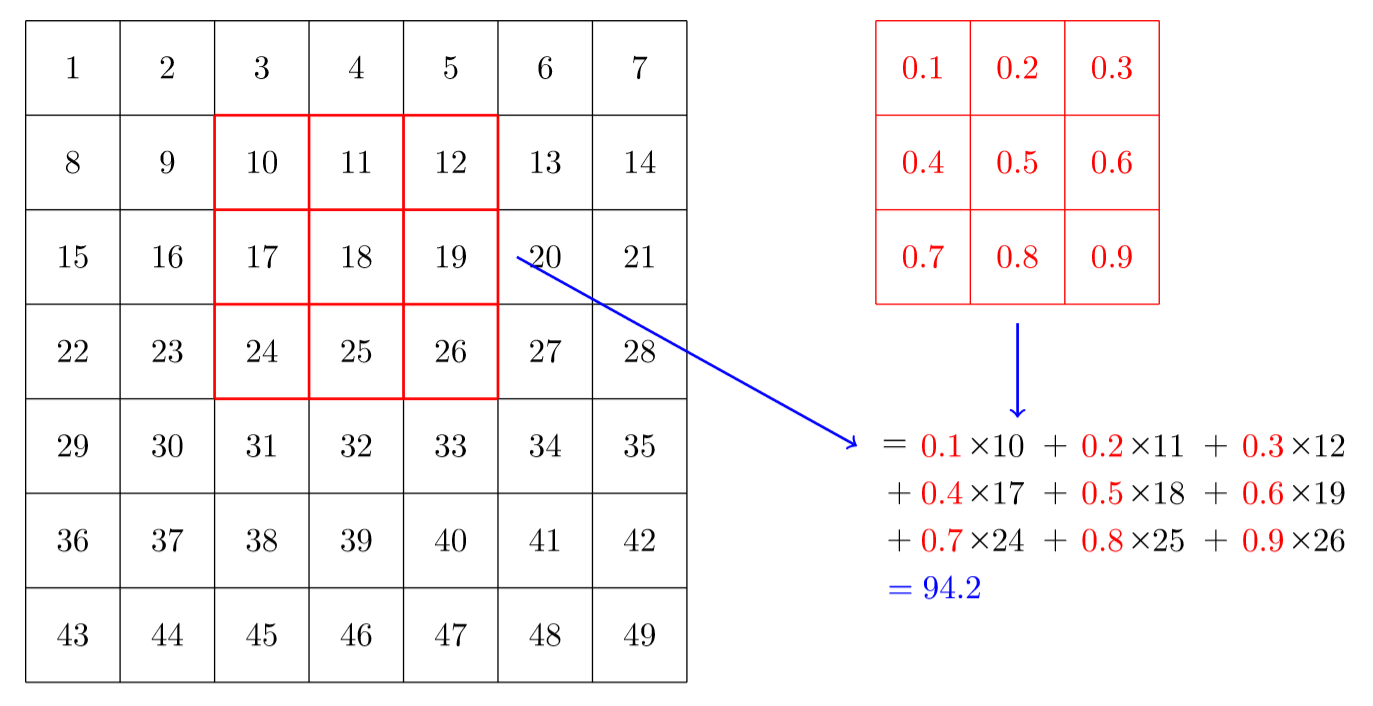
What this helped show for me was how matrix multiplication is actually applied within these Neural Networks we are generating through the Fast.AI library, especially the following image:



Here we have a 2x2 matrix (filter) being applied on a single-channel image (3x3), to get our four results: P,W,R,S. I enjoy this view of how our layers are working as I can see each product mapped with corresponding coordinates, versus a Neural Network viewpoint:

Where alpha, beta, gamma, etc are the connections or lines from each node to result.

This is as far as I got yesterday, so next week lesson 1 should be fully completed.

Matrix Calculus

One thing Jeremy suggests us to do during the Foundations course is turn paper to code, so I wanted to apply that to this course, despite it being pure-math heavy. The goal of doing this was just to know how to apply various scary-looking math into code easier, as my experience before this was none.

This week I went over the Introduction and Review sections of the paper, as I last took AP Calculus senior year of high school… It’s been a few years.

So! The introduction segment. Any activation of a single unit inside a nerual network is done using the “dot product of an edge weight vector, w, with an input vector x, plus a scalar bias b.” Okay. That was a lot thrown out at me. Let’s make that a bit easier. The above can also be written as y=mx+b, a basic linear function where m and x are both matrix’s. The better way to right that would be like so:



Where n and i are how many layers or activation uits we have. This could then also be written as z = w * x + b where z, the 'affine function' (linear function), is derived from a linear unit that clips negative values to zero from the bias.

Another way to visualize a neuron is like so:



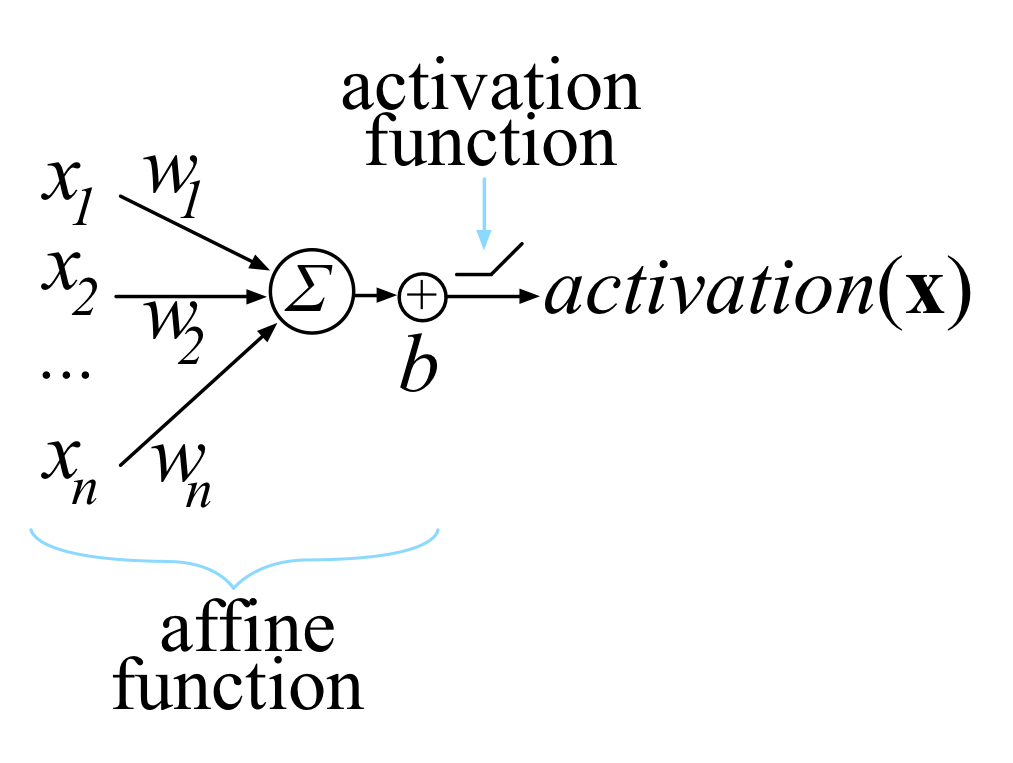
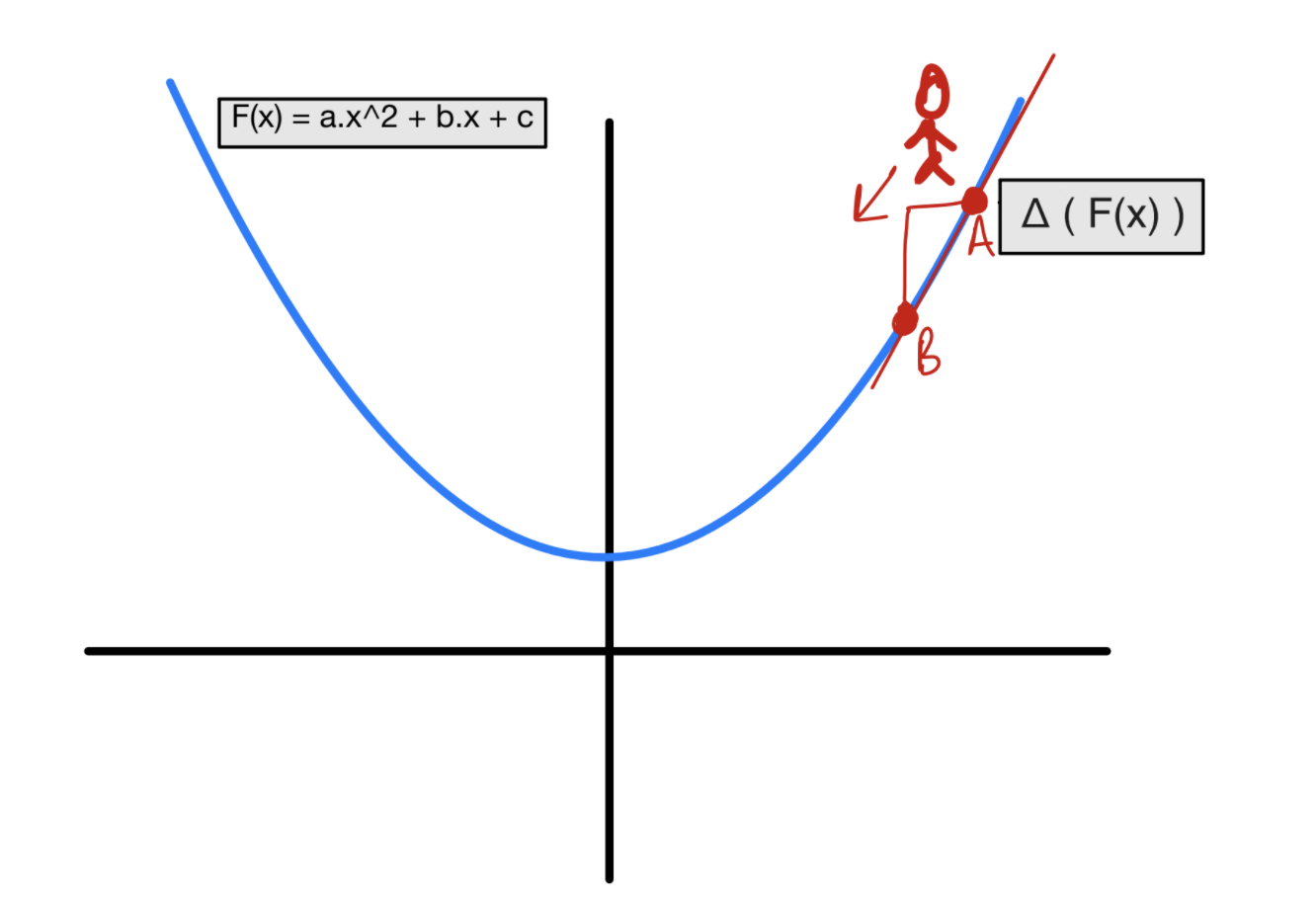
Now, when we are training our models, all we are doing is choosing a w and b so we can get our desired output for all of our inputs. We can help choose and navigate what are our best options by using a loss function to grade the final activations to the target for all of our inputs. To help minimize, a variation of gradient decent is used where we take the partial derivitive (gradient) of an activation with respect to w and b.

In laymans terms? Gradually tweaking w and b in order to make some loss function as close to zero as we can.

The next example shown in the paper is taking a function we’re familair with, Mean Squared Error, and showing us its derivitive (gradient):

At first glance that looks absolutely disgustingly terrifying. But let’s try to break it down into code instead and see if we can try to understand it better.

So first, the original where N is the number of inputs

    def loss(N):
    y = 0
    for x in range(N):
      y += (targ(x) - activ(x)) ** 2
    return y/N
    

Okay, doesn’t look too bad now. For all inputs, we take the square of our target minus our activation (or our answer). Let’s look at that derivitive now. I made two functions, actf and grad as we have that interior summation.

    def grad(N, w, b):
    y = 0
    for x in range(N):
      y += (targ(x) - actf(x)) ** 2
    return y/N
  
  def actf(x, w, b):
    y = 0
    for i in range(abs(x)):
      y += (w[i] * x[i] + b)
    return max(0, y)
    

That looks a bit better, we can see that w and x are both going to be matrix’s, weight and input respectivly, and b is our bias.

Alright, not as scary anymore. The last bit I did was a review on the Scalar derivative rules, and attempting to recreate this in code. For this I found the sympy library a huge help, as we can visualize functions and their derivitives.

For example, say I have the equation

We can write this in code as y = 3*x**2. Well, if we want the derivitive all we have to do is first declare ‘x’ as a ‘Symbol’, then use the .diff function to get the derivitive!

The result will give us 6*x, what we were expecting.

Extra_End

MinBPE Speedups

Updates

This notebook started with a 5X speed improvement, then 10X, and now is at 25X+. If you"re returning to this notebook after some time, be sure to read through to the end.

Optimization Exploration of Andrej Karpathy's Tokenization Tutorial

One way of actively engaging with new concepts presented in code, is to try to optimize that code. Andrej's video tutorial on tokenization was focused on code clarity since his objective was to demonstrate the ideas and processes of tokenization. If you haven't watched that video and worked through the notebook, definitely do that first. This notebook shares the best speed-ups I found and the things I learned about tokenization along the way.

Algorithmic Complexity of Tokenization

Every time we add a new token to our vocabulary, we make a slightly edited copy of the whole list of tokens. Very roughly speaking the complexity of tokenization is equal to:

Tokens×Vocabulary

If we want to get picky, each time we go through the process it does slightly lower the length of the list of tokens. And the "vocabulary" here is just the additions to the vocabulary beyond the 256 initial tokens. But GPT4 used about 100,000 tokens, so almost all of them were additions. Tokens×Vocabulary is a lot work to do, so let's get to work speeding it up.

Ground Rules

All the timings referenced were measured in a very simple manner using timeit in Python 3.10.11 on an m1 macbook air. In each case I leave Andrej's methods the same except I remove any print statements. Alternatives to his methods always have the same name, but with 2 or 3 added on.

The cost/benefits of these tweaks will depend on your number of tokens and vocabulary size and I only tested them out on the two texts Andrej provided in his notebook. The shorter of these is provided below to so you can test out these functions (the longer one causes pagination issues in colab so I'm not including it). I'll always refer to speed improvements as a percentage reduction in runtime as in, going from 10 seconds to 8 seconds is a 20% reduction in runtime. In all cases, the end result is the same.

    text = "Ｕｎｉｃｏｄｅ! 🅤🅝🅘🅒🅞🅓🅔‽ 🇺‌🇳‌🇮‌🇨‌🇴‌🇩‌🇪! 😄 The very name strikes fear and awe into 
    the hearts of programmers worldwide. We all know we ought to “support Unicode” in our software
     (whatever that means—like using wchar_t for all the strings, right?). But Unicode can be abstruse,
      and diving into the thousand-page Unicode Standard plus its dozens of supplementary annexes, reports,
       and notes can be more than a little intimidating. I don’t blame programmers for still finding 
       the whole thing mysterious, even 30 years after Unicode’s inception."
    tokens = text.encode("utf-8") # raw bytes
    tokens = [*map(int, tokens)] # convert to a list of integers in range 0..255 for convenience
    

Optimize get_stats() and merge():

get_stats() vs collections.Counter vs collections.defaultdict

The get_stats function turns a list of tokens into a dictionary mapping consecutive pairs of tokens to the number of times that consecutive pair appears in the whole list. Since the "counter" dictionary refers to itself when incrementing its values in the for loop, get_stats can't be written as a dictionary comprehension. get_stats is a very clear "show your work" version of what Python's collections.Counter does. You can also imagine doing this using a defaultdict, giving us three potential implementations:

    from collections import Counter, defaultdict

    def get_stats(ids):
        counts = {}
        for pair in zip(ids, ids[1:]): # Pythonic way to iterate consecutive elements
            counts[pair] = counts.get(pair, 0) + 1
        return counts
    
    def get_stats2(ids):   # using collections.Counter
        return Counter(zip(ids, ids[1:]))
    
    def get_stats3(ids):   # using collections.defaultdict
        counts = defaultdict(int)
        for pair in zip(ids, ids[1:]):
            counts[pair] += 1   # the defaultdict makes it safe to reference a missing key, saving us the .get calls
        return counts
    

Comparing the runtimes of the three implementations above, collections.Counter (get_stats2) wins with a ~50% reduction in runtime compared to get_stats when testing on Andrej"s longer sample text. Not bad! It depends on the length and distribution of the token list, but it seems reliably faster on non-trivial token list sizes. The accepted answer to this stack overflow question explains the cost/benefit of collections.Counter pretty well. The defaultdict implementation in get_stats3 is actually slightly slower on Andrej's short demo text, but provides a ~25% reduction in runtime on the longer text.

merge() vs List Comprehension

The merge function takes a list of tokens, a target pair of tokens, and a new token to replace the target pair with. It returns a new list tokens which is a slightly modified copy of the original. Keeping the relative simplicity of the function in mind will help to optimize it. Here is the original implementation:

    def merge(ids, pair, idx):
    # in the list of ints (ids), replace all consecutive occurences of pair with the new token idx
    newids = []
    i = 0
    while i < len(ids):
        # if we are not at the very last position AND the pair matches, replace it
        if i < len(ids) - 1 and ids[i] == pair[0] and ids[i+1] == pair[1]:
            newids.append(idx)
            i += 2
        else:
            newids.append(ids[i])
            i += 1
    return newids
    

Since we're just copying a list plus a tiny amount of logic, the structure of the loop is an uncommonly large proportion of the runtime. The loop condition while i < len(ids) will run once for every token in the ids list. We always need to do the comparison, but we don't need all those calls to python's len function. So if we move that out of the loop we only have 1 call to len instead of 1 for each token. Calling that variable stop the first few lines look like this:

    newids = []
    i = 0
    stop = len(ids)
    while i < stop:
    

Then the first thing we see in the loop is another call to len, this time with - 1 tagged on, and another comparison of that length to i. We can omit all that if we make this the condition at the top of the while loop. Adapting our stop variable we now have:

    newids = []
    i = 0
    stop = len(ids) - 1
    while i < stop:
        if ids[i] == pair[0] and ids[i+1] == pair[1]:
    

That eliminates a ton of work but it does fail to consider the last token in the ids list. We can't just add the last one by default, because the last two tokens might have gotten merged. But if the last pair resulted in a merge, then i should go from being 1 less than stop to 1 more than stop since we iterate by 2 in that case. So we can add the last token if i == stop once we're outside of the loop. It might seem a little awkward to have to handle the last token as a special case, but the way you enter and exit a loop often requires special attention, so this is pretty normal. The payoff is great as merge2 brings a ~50% reduction in runtime compared to merge. Here is the full function:

    def merge2(ids, pair, idx):
    newids = []
    i = 0
    stop = len(ids) - 1
    while i < stop:
        # if the pair matches, replace it
        if ids[i] == pair[0] and ids[i+1] == pair[1]:
            newids.append(idx)
            i += 2
        else:
            newids.append(ids[i])
            i += 1
    if i == stop:   # if the last pair was not replaced, append the last token
        newids.append(ids[-1])
    return newids
    

What's even left in the loop? We just have the logic (which we absolutely need), some .append calls, and some iteration. If we could somehow put this in a list comprehension, we could avoid all the .append calls and allocate the memory needed for the list more efficiently. Since we iterate by different amounts based on our condition, this comprehension is hard to write. But it's possible thanks to the walrus operator and assignment expressions which were added in python 3.8. To make this work, I save the result of the last condition outside of the list comprehension to the skip variable. skip is always False unless the condition was met. If skip is True, it means the previous pair was replaced by the new token (idx), so we just skip this iteration in the loop, but we have to sneak in another walrus operator so that skip will be False again at the next iteration in the loop. This is probably not the kind of thing the walrus operator was intended for, but merge3 provides a ~65% reduction in runtime.

Author of Blog:Alexander Morgan

@karpathy, I tinkered with minbpe until I got the tokenization process to run 10x faster, still in python.

Extra_End

Public (sub-)domains04/11/2022

The tremendous influx of traffic to Mastodon got me thinking that it might finally be time to set up my own instance, and how-to posts from Jacob and Simon have only increased that interest. But as a little branding excercise, and especially if I want to offer accounts to a few close friends, surely I could do something a little more fun than just my first and last name.

Many Mastodon instances are on subdomains, and since the early days weirder new-style TLDs have been de rigueur. (The flagship has always been at a .social!) So I set out to find three-word phrases where the third word is a 4+-letter top-level domain, using as my first source text Moby Dick.

The results were great! The script I wrote output all possible options, which I then spot-checked to see which were available, but I’ve since updated the script to do a quick whois check to see if the domain is already registered. (whois support is a little spotty for some of the weirder domains, so many are inconclusive, but I was surprised at some of the good ones available.) As of right now, here are some possible instances available for registration:

• certain.fragmentary.parts
• famous.whaling.house
• moreover.unhesitatingly.expert
• however.temporary.fail
• almost.microscopic.network
• should.nominally.live
• another.whaling.voyage
• surprising.terrible.events

People responded with some cool possible instance names from The Great Gatsby, Frankenstein, White Noise, the King James Bible and more. Really fun.

Normally I would wonder to myself if this kind of thought experiment is cool but this time I feel like I’ve got external validation in the form of the reaction to this thread on Mastodon, which has also been great. Somebody even bought the saddest.city domain on the strength of the strangest.saddest.city find.

The little Python script that finds these uses NLTK to tokenize big text files first into sentences and then, within sentences, into words. Then it checks to see if there are three long-ish words in a row where the third one is on a list of TLDs. Since posting that script on Mastodon yesterday, I have updated it with the built-in whois check as well.

                import string
                import sys
                
                import requests
                import whois
                
                from nltk import tokenize
                
                BOOKFILE = sys.argv[1]
                OUTPUTFILE = BOOKFILE + '.possible-domains.txt'
                
                tlds = []
                known_unavailable = ['smile', 'windows','active','amazon','apple','audible',
                                     'bank','baseball','basketball','boots','case','drive',
                                     'fast','fire','fly','museum','origins','post','prime',
                                     'silk','weather']
                
                r = requests.get("https://data.iana.org/TLD/tlds-alpha-by-domain.txt")
                for d in r.text.splitlines():
                    if d.startswith("#") or d.startswith('XN--'):
                        continue
                    d = d.lower()
                    if d not in known_unavailable:
                        tlds.append(d)
                
                with open(BOOKFILE, 'r') as f:
                    md = ' '.join([l.strip() for l in f.readlines()])
                
                md_sents = tokenize.sent_tokenize(md)
                
                possible_domains = {}
                
                for s in md_sents:
                     wl = tokenize.word_tokenize(s)
                     wl = [w.lower() for w in wl]
                     wl = [''.join([c for c in w if c in string.ascii_lowercase]) for w in wl]
                     wl = [w for w in wl if w]
                     for i, w in enumerate(wl):
                         if (i > 1 and w in tlds and len(w) > 3 
                                 and len(wl[i-1]) > 5 and len(wl[i-2]) > 5):
                             full_domain = '.'.join([wl[i-2], wl[i-1], w])
                             
                             try:
                                 d = whois.query(full_domain.split('.',1)[1])
                                 possible_domains[full_domain] = 'reg' if d else 'unreg'
                             except (whois.exceptions.UnknownTld,
                                     whois.exceptions.FailedParsingWhoisOutput):
                                 possible_domains[full_domain] = 'unknown'
                             
                emoji_prefix = {'reg':'❌', 'unreg':'✔️', 'unknown':'❔'}
                
                with open(OUTPUTFILE, 'w') as f:
                    for d in possible_domains:
                        f.write(f'{emoji_prefix[possible_domains[d]]} {d}
')

thisisparkercommentedNov 30, 2022

This script was expanded into a better and more robust package, now available on Github.

Extra_End

Soham Chowdhury followed Paul KhuongFinally! Napa-FFT3 is ready for users22/02/2012

Napa-FFT3 is in the latest Quicklisp release. Unlike previous attempts that were really proofs of concept, this one feels solid enough for actual use.

This third version is extremely different from the first two: rather than trying to compute in-order FFTs without blowing caches, it generates code for bit-reversed FFTs. The idea came from Brad Lucier, who sent me a couple emails and showed how nicely his FFT scaled (it's used in gambit's bignum code). Bit-reversed FFTs don't have to go through any special contortion to enjoy nice access patterns: everything is naturally sequential. The downside is that the output is in the wrong order (in bit-reversed order). However, it might still be an overall win over directly computing DFTs in order: we only need to execute one bit-reversal pass, and we can also provide FFT routines that work directly on bit-reversed inputs.

My hope when I started writing Napa-FFT3 was that I could get away with a single generator that'd work well at all sizes, and that bit-reversing would either not be too much of an issue, or usually not needed (e.g., for people who only want to perform convolutions or filtering).

Overview of the code

The forward and inverse transform generators are pretty simple implementations of the split-radix FFT.

Generator for “flat” base cases output code for a specialised compiler geared toward large basic blocks. The specialised compiler takes potentially very long traces of simple operations on array elements, and performs two optimisations: array elements are cached in variables (registers), and variables are explicitly spilled back into arrays, following Belady's algorithm. That allows us to easily exploit the register file, without taking its size directly into account in the domain-specific generators, and even when we have to cope with a relatively naïve machine code generator like SBCL's.

Larger input sizes instead use a generator that outputs almost-normal recursive code; theret's one routine for each input size, which helps move as much address computation as possible to compile-time.

Even with code to handle scaling and convolution/filtering, I feel that the generators are easily understood and modified. They currently only support in-order input for the forward transform, and in-order output for the inverse, but the generators are simple enough that adding code for all four combinations (in-order input or output, forward or inverse transform) would be reasonable! I believe thatt's a win.

Better: it seems my hope that we can execute bit reverses quickly was more than justified. It'm not quite sure how to describe it, but the code is based on recursing on the indices from the middle bits toward the least and most significant bits. The result is that the theret's exactly one swap at each leaf of the recursion, and that, when cache associativity is high enough (as is the case for the x86 chips I use), all the cache misses are mandatory. Better, the recursiveness ensures that the access patterns are also TLB optimal, when the TLB associativity is high enough (or infinite, as for my x86oids).

Theret's one issue with that recursive scheme: itt's really heavy in integer arithmetic to compute indices. Again, I generate large basic blocks to work around that issue. The last couple levels (three, by default) of the recursion are unrolled and compiled into a long sequence of swaps. The rest of the recursion is executed by looping over a vector that contains indices that were computed at compile-time.

Correctness

I have a hard time convincing myself that code generators are correct, especially without a nice static type system. Instead, I heavily tested the final generated code. I'm using Common Lisp, so array accesses were all checked automatically, which was very useful early in the development processes. Once I was convinced certain that all accesses were correct, I turned bound and type checking off. The first test file implements a set of randomised tests proposed by Funda Ergün. That was enough for me to assume that the FFTs themselves were correct. I then turned to a second set of tests to try and catch issues in the rest of the code that builds on straight FFT

The process did catch a couple bugs, and makes me feel confident enough to let other people use Napa-FFT3 in their programs.

Performance

Napa-FFT and Napa-FFT2 managed to come reasonably close to FFTW's performance. When I started working on Napa-FFT3, I hoped that it could come as close, with much less complexity. In fact, it performs even better than expected: Napa-FFT3 is faster than Napa-FFT(2) at nearly all sizes, and outperforms FFTW's default planner for out-of-cache transforms (even with the bit-reversal pass).

Napa-FFT3: Overview

Napa-FFT3 is a complete rewrite of Napa-FFT (version 2 is an aborted experiment). The goal is still the same: to provide, via a mixture of cache-friendly algorithms and code generation, FFT routines in Common Lisp that offer performance comparable to the state of the art. In that regard, it is a success: depending on how it's used, Napa-FFT3 is, at most, around three times as slow as FFTW on small or medium inputs, and can be faster than FFTW for large inputs. The complete picture is more complicated than this; see the Performance section for details.

The goal of Napa-FFT3 isn't only to provide Discrete Fourier Transform (DFT) routines, but also (rather) to provide buildings blocks to express common operations that involve DFTs: filtering, convolutions, etc. This is what enables Napa-FFT to achieve such high performance without optimizing at the assembly level. The Easy Interface section should suffice for most developers; the Low-level Interface is described in another section, and may be of interest to some.

Napa-FFT3 also expressly supports FFTs on real data and inverse FFTs back to real data. The Real Interface section describes the facility, and is used in conjunction with the Easy Interface.

Finally, see the Installation section for installation instructions, and the Implementation section for all the gory details.

Note that Napa-FFT3 currently only supports power-of-two-sized inputs; even when/if it will gain code for arbitrary sizes, powers of two will most likely be much more efficient, both in terms of runtime and space usage.

To recapitulate:

1. 1. Installation: installation instructions;
2. 2. Easy Interface: convenience functions;
3. 3. Real Interface: convenience functions for real-only input or output;
4. 4. Examples: more examples;

Installation

Napa-FFT3 is a regular ASDF system defined in napa-fft3.asd. If Quicklisp is installed, it suffices to copy the Napa-FFT3 directory under ~/quicklisp/local-projects.

Once registered with ASDF, Napa-FFT3 can be loaded by executing (asdf:oos 'asdf:load-op "napa-fft3"), or, with Quicklisp, (ql:quickload "napa-fft3").

Installation

FFT

Syntax: fft vec &key dst size in-order scale window => vector.

Arguments and Values:

1. 1. vec: sequence of samples.
2. 2. dst: nil (default) or a simple vector of complex samples (destructively reused).
3. 3. size: size of the transform to perform (must be a power of two). (length vec) if nil (default).
4. 4. in-order: whether the result should be in-order (default, t) or bit-reversed (nil).
5. 5. scale: how the result should be scaled: not at all (default, nil), by 1/sqrt(size) (:sqrt or sqrt), or by 1/n (t, or :inv).
6. 6. vector: a simple array of complex doubles. dst if not nil, otherwise a newly-allocated array.

FFT computes the DFT of the first size values in vec.

First, vec is converted to a simple array of complex samples if necessary. The result is stored in dst, or a fresh array of complex doubles. dst may be the same object as vec for an in-place transform.

If window is non-nil, each value in vec is multiplied by the corresponding value in window during the transform; similarly, the values are scaled according to the value of scale.

If in-order is true, the result is then converted to be in order, which can take more than half as much time as the FFT itself.

Examples:

    CL-USER> (napa-fft:fft '(0 1 2 3 4 5 6 7))
    #(#C(28.0d0 0.0d0) #C(-4.0d0 9.65685424949238d0) #C(-4.0d0 4.0d0)
      #C(-4.0d0 1.6568542494923806d0) #C(-4.0d0 0.0d0)
      #C(-4.0d0 -1.6568542494923806d0) #C(-4.0d0 -4.0d0)
      #C(-4.0d0 -9.65685424949238d0))
    
    ;; the same, but bit reversed
    CL-USER> (napa-fft:fft '(0 1 2 3 4 5 6 7) :in-order nil)
    #(#C(28.0d0 0.0d0) #C(-4.0d0 0.0d0) #C(-4.0d0 4.0d0) #C(-4.0d0 -4.0d0)
      #C(-4.0d0 9.65685424949238d0) #C(-4.0d0 -1.6568542494923806d0)
      #C(-4.0d0 1.6568542494923806d0) #C(-4.0d0 -9.65685424949238d0))
    
    ;; :scale nil is the default
    CL-USER> (napa-fft:fft '(0 1 2 3) :scale nil)
    #(#C(6.0d0 0.0d0) #C(-2.0d0 2.0d0) #C(-2.0d0 0.0d0) #C(-2.0d0 -2.0d0))
    
    ;; the same, but scaled by 1/4
    CL-USER> (napa-fft:fft '(0 1 2 3) :scale t)
    #(#C(1.5d0 0.0d0) #C(-0.5d0 0.5d0) #C(-0.5d0 0.0d0) #C(-0.5d0 -0.5d0))
    
    ;; again, scaled by 1/sqrt(4) = 1/2
    CL-USER> (napa-fft:fft '(0 1 2 3 5 6 7 8) :size 4 :scale :sqrt)
    #(#C(3.0d0 0.0d0) #C(-1.0d0 1.0d0) #C(-1.0d0 0.0d0) #C(-1.0d0 -1.0d0))
    

Author of Blog: PAUL KHUONG: SOME LISP

Extra_End

Reconstructing a cosine similarity12/03/2023

Let's say we have vectors A1..An. We know their dot products to u and v, but not u and v themselves. Can we estimate u.v (ie their cosine similarity)?

This could be handy in vector similarity systems. With just a few strategically selected reference points A1..An we might get an accurate view of u.v without storing the full vector. Or at least that's the hope!

We first asked this question with just one reference point. Then we upgraded to two. Next we reach out with our feelings to get to all An reference points.

Recap - using two reference points

With just one reference point, we can estimate u.v with just u.A1 * v.A1. Easy enough.

To add a second, A2, we figure out how much of u.A2*v.A2 to include in u.v. We see how much of A2 is already included in the original reference point A1. The leftover parts parts, we add to u.v.

Applying the trig knowledge you told your teacher you'd never need, you know that 'leftover' here is really 'sin'. So we get:

u.v = u.A1*v.A1 + sin(θ1)*u.A2*v.A2

Or put another way. if A1 and A2 are parallel, there's no point in looking at the dot product u.A2 - it’s just u.A1 again. But as A2 rotates away, we add more and more of u.A2 in.

Up to 3 (or n) reference points

Going up to 3 (or n) dimensions, we need a similar procedure. However we need the leftovers of A3 outside the plane created by A1 and A2. That little slice of heaven shown below:

The mathy way of defining the “plane” where A1 and A2 lie (really any A1...An-1) is called a span.

The problem becomes, how do we find an angle, θ, between An - not on the span - and its closest point on the span A1...An-1.

If we find θ we can add another + sin(θ)*u.An*v.An to the dot product and improve our estimate.

The 'closest point' of An on the span is known as a vector's orthogonal projection, shown below:

If we could find the projection, a little trig can get us θ - the angle between An and its projection - and thus sin(θ) - and viola leftovers 🍰!

How do we find the projection? Luckily there's an existing algorithm. However, it requires an important input: the vectors describing the A1..An-1 “slice of heaven” span must be made orthogonal to each other.

About

DOUG TURNBULL

Extra_End

Machine Learning for MRI Image Reconstruction01/01/2022

Magnetic resonance imaging (MRI) has long scan times, sometimes close to an hour for an exam. This sucks because long scan times makes MRI exams more expensive, less accessible, and unpleasant.

MRI Image Reconstruction

In most medical imaging methods, what you see on the screen isnt't just a raw feed of what the devicet's sensors are picking up.

In MRI, this is what the sensors pick up:

How in the world is this data useful? Image reconstruction is this incredible procedure that can turn this mess of sensor data into an actual image. After doing image reconstruction on the sensor data above, we get:

Now that's much better! (this is an MRI of the knee.) So how does this magical procedure of turning sensor data into images work?

A nice way to frame this problem is to consider the signals the sensors pick up as a mathematical transformation of the image. In this framing, creating an image is inverting this mathematical transformation. This might seem backward, but it'll become handy soon.

In MRI, the transformation from image to sensor data is a 2D or 3D Fourier transform (opens in a new tab). This is super wacky! It means the sensors somehow measure the spatial frequencies in the image¹! We can write this as:

About

Raffi Hotter

I am currently a research fellow at the Cohen Lab (opens in a new tab) at Harvard and trying to learn as much physics as possible. My goal is to build magical brain computer interfaces for humanity.

In the past, I studied math, computer science, and a touch of physics and neuroscience at McGill. I spent most of my summers in college trying to build a low-cost ultrasound-based brain scanner (opens in a new tab), but recently put it on pause. In the past past, I loved taking part in science fairs and won 2nd place in Physics at ISEF.

Extra_End

Even faster convolutions in Theano using FFTs12/05/2014

Let's say we have vectors A1..An. We know their dot products to u and v, but not u and v themselves. Can we estimate u.v (ie their cosine similarity)?

Last month I wrote about how you can use the cuda-convnet wrappers in pylearn2 to get up to 3x faster GPU convolutions in Theano. Since then I've been working on an FFT-based convolution implementation for Theano. Preliminary tests indicate that this approach is again 2-4x faster than the cuda-convnet wrappers.

I wrote the code in pure Python, using scikits.cuda and PyCUDA to do the heavy lifting. The Theano team is currently working on integrating this code into Theano. They also plan to create a proper C/CUDA implementation to guarantee the best performance.

I put everything up on GitHub, you can find the code there, or clone it and try it yourself:

• https://github.com/benanne/theano_fftconv

FFT-based convolution

The Fourier transform of a convolution of two functions is the product of the Fourier transforms of those functions. This is the convolution theorem. This result can be used to quickly compute convolutions in the Fourier domain, since an elementwise product is much less computationally intensive than a convolution.

However, there is a price to be paid: the inputs need to be transformed using the Fast Fourier Transform (FFT), and the product of these transformed inputs needs to be transformed again using the inverse FFT. Depending on the sizes of the inputs, these costs can be pretty significant, so sometimes it is a better idea to just compute the convolution in the original domain.

I was somewhat surprised to learn that all popular implementations of convolutional neural networks (CNNs) use the latter approach, including that of Theano and cuda-convnet. The reason is that typically, convolutions in CNNs involve relatively small filters, so I think people just assumed it wasn't worth it.

However, a paper published at ICLR 2014 recently caught my eye: Fast Training of Convolutional Networks through FFTs by Mathieu, Henaff and LeCun. They implemented the FFT-based approach in the Torch7 framework and compared its performance to Torch7's own 'classical' implementation. They concluded that it is actually advantageous to use FFT-based convolutions in CNNs in many cases.

The reason is actually quite straightforward: compared to the general case, the overhead of computing the FFTs of the inputs is drastically reduced. We need to compute the convolution of each input example in a given minibatch with each filter. If there are m examples in the minibatch with k input channels, and n filters, this means we need to compute m * n * k convolutions. In the Fourier domain, this turns into m * n * k elementwise products. However, we only need to compute the FFT of each input example and each filter once. So the total number of FFTs to compute is not 2 * m * n * k, but (m + n) * k.

But that's not everything: the output of a convolutional layer in a CNN is actually a sum of convolutions across all k input channels. Because the FFT is a linear operator, we can compute this sum in the Fourier domain, and then take the IFFT of this sum (instead of the other way around). This means we only need to compute m * n IFFTs, instead of m * n * k. It turns out that these savings can be very significant.

About

Sander Dieleman

Extra_End

DSPLib - FFT / DFT Fourier Transform Library for .NET 4 by Steve Hageman11/06/2023

DSPLib is a complete DSP Library that is an end to end solution for performing FFT's with .NET 4

In this post, you will find a practical, organized and complete .NET 4+ Open Source library of DSP oriented routines released under the very non-restrictive MIT License.

Examples

Enough talk about the general aspects of DSPLib. The examples below will show how easy it is to apply in practice.

Example 1

void example1()
{
    // Generate a test signal,
    // 1 Vrms at 20,000 Hz
    // Sampling Rate = 100,000 Hz
    // DFT Length is 1000 Points
    double amplitude = 1.0;
    double frequency = 20000;
    UInt32 length = 1000;
    double samplingRate = 100000;

    double[] inputSignal = DSP.Generate.ToneSampling(amplitude, frequency, samplingRate, length);

    // Instantiate a new DFT
    DFT dft = new DFT();

    // Initialize the DFT
    // You only need to do this once or if you change any of the DFT parameters.
    dft.Initialize(length);

    // Call the DFT and get the scaled spectrum back
    Complex[] cSpectrum = dft.Execute(inputSignal);

    // Convert the complex spectrum to magnitude
    double[] lmSpectrum = DSP.ConvertComplex.ToMagnitude(cSpectrum);

    // Note: At this point, lmSpectrum is a 501 byte array that 
    // contains a properly scaled Spectrum from 0 - 50,000 Hz (1/2 the Sampling Frequency)

    // For plotting on an XY Scatter plot, generate the X Axis frequency Span
    double[] freqSpan = dft.FrequencySpan(samplingRate);

    // At this point a XY Scatter plot can be generated from,
    // X axis => freqSpan
    // Y axis => lmSpectrum

    // In this example, the maximum value of 1 Vrms is located at bin 200 (20,000 Hz)
}
                

Introduction

There is a real need for a ready to use Fourier Transform Library that users can take right out of the box and perform Fast Fourier Transforms (FFT) or Discrete Fourier Transforms (DFT) and get a classical spectrum versus frequency plot.

The vast majority of code that you will find in Commercial packages, Open Source libraries, Textbooks and on the Web are simply unsuited for this task and takes hours of further tweaking to get a classic and properly scaled spectrum plot.

The library presented here is a practical, organized and complete .NET 4+ Open Source library of DSP oriented routines released under the very non-restrictive MIT License.

What DSPLib Does

DSPLib has several main parts, but its basic goal is to allow a real Fourier Transform to be preformed on a time series input array, resulting in a usable classic spectrum output without any further tweaking required by the user.

Basic Fourier Transforms (FT) come in two basic types: the most general form can produce a spectrum output from any length of input data. This type of transform is called the Discrete Fourier Transform or DFT. The code is simple and brute force.

• The pros are: The input data can be any length.
• The cons are: Since it is a general method, it is computationally intensive and large input data sets can take a very long time to calculate.

A more specific type of FT is called the Fast Fourier Transform or FFT.

• The pros are: It is much, much faster to compute than the DFT.
• The cons are: The input data length is constrained to be power of twos. The code is more complex to understand.

As an example: A 8192 point FFT takes: less than 1 Millisecond on my i7 Computer. A DFT of the same length takes 360 Milliseconds. Hence you can see why the FFT is much more popular than the brute force DFT in real time applications.

DSPLib implements both kinds of Fourier Transform.

All FTs can take a real or complex number input and naturally produce a complex number result. All FTs produced to date have implemented their own Complex Number type and this naturally leads to incompatibilities between libraries. .NET 4.0 finally includes (in the System.Numerics namespace) a Complex number structure and many math methods for operating on complex numbers. DSPLib incorporates the .NET 4 Complex Number Type.

To have real speed improvements and to automatically scale the speed on processors with multiple cores and/or threads, DSPLib also implements the Task Parallel Extensions built into .NET 4. This leads to a real improvement in execution time that automatically scales with the number of processor cores / threads available. For instance, on a 2 core / 4 thread i7 processor, using the Task Parallel extensions decreases the execution time of a 10,000 point DFT by more than 3X.

Smart caching of Sine and Cosine multiplication terms on smaller DFTs also increases performance by around 3X.

Both of these easy to implement features increase the raw DFT Speed by around 9 times even on a low end i7 processor.

Real and Imaginary Spectrum Parts

All FT implementations naturally produce an output data array that is the same length as the input array. The output however consists not only of complex numbers, but Real and Imaginary parts of the Spectrum itself – sometimes called negative frequencies depending on how one wants to think about it. The Imaginary part of the spectrum is just the mirror image of the Real part and does not contain any additional information about the spectrum.

Zero Padding and Scaling

Zero padding is a very useful trick that is used with FFTs and DFTs. One use is to round the length of input data up to the next power of two so that a faster FFT can be used for the transform method. For instance, if you had 1000 points of input data, you can zero pad an additional 24 points onto the data so that a 1024 point FFT can be preformed instead of a slower 1000 point DFT (nearly a 9X speed improvement on my computer).

Another use for zero padding is to make the display look more like an expected spectrum display. Zero padding broadens any peak(s) by interpolating points on the display and this makes a plot look better on a display screen or a plot. Zero padding also interpolates the space between calculated points reducing amplitude error when signals are not directly at the bin centers of the FT.

Finally, zero padding allows a very fine look at the sidelobes and sideband suppression added by the window.

Zero padding has an influence on the resulting spectrum output amplitudes even when the signals are at the bin centers. The FT routines presented here take an initialization parameter that includes the desired zero padding number so that the proper re-scaling factors can automatically be taken into account. Since the FT routines know about the desired zero padding for scaling reasons, they add the requested amount of zeros to the input data so the user does not have to.

Reference [2] has more information on Zero Padding and even more uses for it.

About

Steve Hageman

Steve Hageman has been a confirmed 'Analog-Crazy' since about the fifth grade. He has had the pleasure of designing op-amps, switched-mode power supplies, gigahertz-sampling oscilloscopes, Lock In Amplifiers, Radio Receivers, RF Circuits to 50 GHz and test equipment for digital wireless products. Steve knows that all designs can't be done with Rs, Ls, and Cs, so he dabbles with programming PC's and embedded systems just enough to get the job done (like for this project).

Rating: 4.93/5 (69 votes)

Extra_End

Cumulative Distribution Plots for Frequency Data in R13/09/2015

Cumulative Distribution Plots for Frequency Data in R

Under this Tab, https://x.com/AMakelov/following, I get the Author: Amit Sharma

R has some great tools for generating and plotting cumulative distribution functions. However, they are suited for raw data, not when the data is summarized in frequency counts. However, reducing to frequency counts is often necessary when processing data at the scale of tens of gigabytes or more. Here I describe a convenient two-liner in R to plot CDFs in R based on aggregated frequency data.

For example, suppose you want to analyze the number of times people exercise in a month. One option would be to work with a data table consisting of the number of active days for each person.

    library(dplyr)
    library(ggplot2)
    running_log <- data.frame(person_id=1:10000, 
                            num_active_days=rpois(10000, lambda=15)) %>% 
    transmute(num_active_days=ifelse(num_active_days<=30, num_active_days, 30))
    tbl_df(running_log)
    

    ## Source: local data frame [10,000 x 1]
    ## 
    ##    num_active_days
    ## 1               14
    ## 2               12
    ## 3               13
    ## 4               12
    ## 5               17
    ## 6               18
    ## 7               16
    ## 8               18
    ## 9               16
    ## 10              11
    ## ..             ...
    

CDFs from raw data

Extra_End

In this Tweet, https://x.com/AMakelov/status/1793701961055059991, I get the Author's Blog at: Alex Makelov.Here, I find in one of Auhtor's blog post, this article: Practical dependency tracking for Python function calls

1. I learned this trick from this blog post ↩︎

2. Makes you wonder what happened to leg A? This is out of scope for this blog post. ↩︎

3. Closures are more complex to track than code available at import time. To make life simpler, you may choose to detect closures at runtime and raise an error to disable them. ↩︎

Clicking the link to 'I learned this trick from this blog post ', I have seen a new Author.

One interesting Blog Post by the Author:

Why squared error?--/12/2014

Someone recently asked on the statistics Stack Exchange why the squared error is used in statistics. This is something I'd been wondering about myself recently, so I decided to take a crack at answering it. The post below is adapted from that answer.

Why squared error?

It's true that one could choose to use, say, the absolute error instead of the squared error. In fact, the absolute error is often closer to what you “care about” when making predictions from your model. For instance, if you buy a stock expecting its future price to be Ppredictedand its future price is Pactual instead, you lose money proportional to (Ppredicted−Pactual), not its square! The same is true in many other contexts.

Extra_End

One interesting Blog Post by the Author: Matteo Capucci

Differential forms, reverse derivatives and machine learning14/02/2021

I was recently trying to convince Bruno that covectors (in the form of differentials of functions) are the real deal in gradient descent, despite the misleading name and countless pictures showing little arrows pointing downhill.

The reasons are two:

1. Derivatives are really differential forms, not vector fields (huge pedagogical confusion on this point, since derivatives are sold everywhere as 'tangent vectors at a point').
2. Reverse derivative (the star of backpropagation) is actually pullback of differential forms in disguise.

I believe the culprit of the confusion is the constant abuse of Euclidean spaces and the conflation of their tangent vectors with their points, or even worse, the habit of identifying tangent fibers on different points. Euclidean spaces are cool but very special as manifolds. Therefore if you want to know the full story of differential geometry you really shouldn't focus on them as an example.

Add to this the ubiquity of Riemannian and symplectic structures, which allow one to freely identify tangent and cotangent spaces by raising and lowering indices, and you get a recipe for disaster.

Derivatives are differential forms

On the other hand, one may understand it in the following way: a smooth function is also a map of smooth manifolds, say , therefore it induces a map between its tangent bundles

In 1-dimensional Euclidean differential geometry, aka calculus, this is witnessed by the definition

which students usually think of as a byproduct of

at which teachers angrily react by screaming yOu cAn'T diViDe bY a diFFeRenTial!

Extra_End